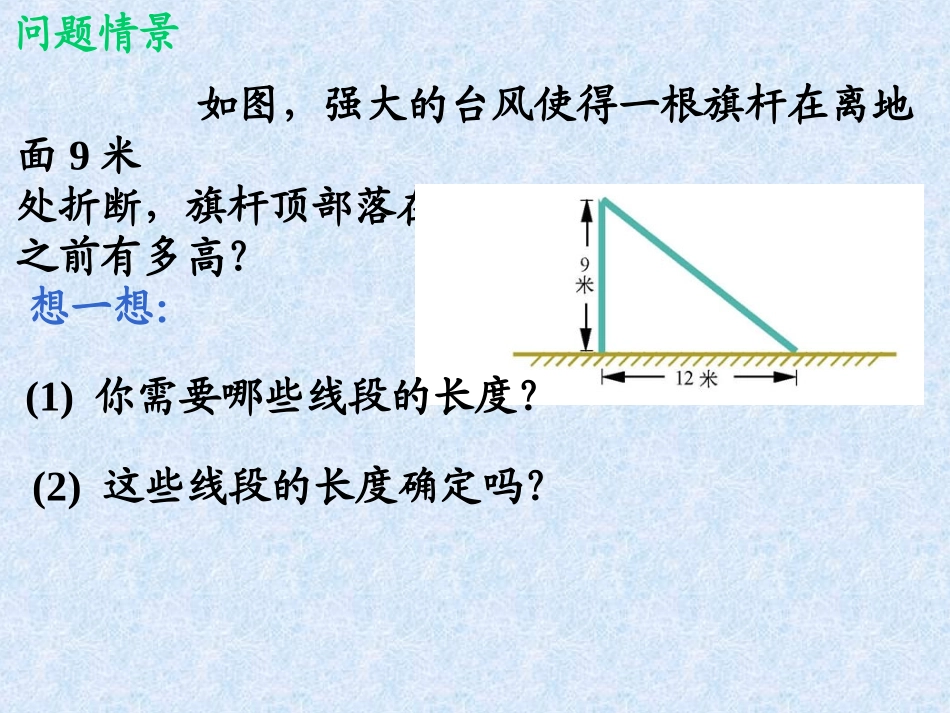
北师大版八年级(上)1.1探索勾股定理(1)1.1探索勾股定理(1)科学家曾经建议用“勾股定理”的图来作为与“外星人”联系的信号。勾股定理有着悠久的历史,古巴比伦人和古代中国人看出了这个关系。新知导入古希腊的毕达哥拉斯学派首先证明了这个关系。“勾股定理”图问题情景如图,强大的台风使得一根旗杆在离地面9米处折断,旗杆顶部落在离旗杆底部12米处。旗杆之前有多高?想一想:(1)你需要哪些线段的长度?(2)这些线段的长度确定吗?合作交流(1)在纸上作出若干个直角三角形,分别测量它们的三条边长,看看三边长的平方之间有什么样的关系?两直角边的平方和等于斜边的平方三边长的平方之间的关系:测量法合作交流(2)如图,直角三角形三边的平方分别是多少,它们满足上面所猜想的数量关系?你是如何计算的?ⅰ、三边的平方分别是各正方形的面积;ⅱ、满足“两直角边的平方和等于斜边的平方”。数格子法合作交流(3)如图,直角三角形三边的平方分别是多少,它们满足上面所猜想的数量关系?你是如何计算的?ⅰ、三边的平方分别是各正方形的面积;ⅱ、满足“两直角边的平方和等于斜边的平方”。数格子法巩固练习1、求下图中字母所代表的正方形的面积:合作交流(4)如果直角三角形的两直角边分别为1.6个单位长度和2.4个单位长度,上面所猜想的数量关系还成立吗?说明你的理由。1.62.4合作交流合作交流(4)如果直角三角形的两直角边分别为1.6个单位长度和2.4个单位长度,上面所猜想的数量关系还成立吗?说明你的理由。1.62.4勾股弦较短的直角边称为“勾”较长的直角边称为“股”斜边边称为“弦”仍然成立新知归纳勾股定理:(1)文字语言:直角三角形两直角边的平方和等于斜边的平方。ABCabc(2)符号语言:90C222cba(已知)(勾股定理)拓展阅读拓展阅读问题解决如图,强大的台风使得一根旗杆在离地面9米处折断,旗杆顶部落在离旗杆底部12米处。旗杆之前有多高?∴斜边=15∴旗杆高=9+15=24(米)∵92+122=斜边2在直角三角形中:新知归纳“勾股定理”的应用:ABCabc已知直角三角形两边,求第三边。a2+b2=c2a2=c2-b2b2=c2-a2巩固练习2、求下列直角三角形未知边的长度:513y68x先明确斜边巩固练习3、小明妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?巩固练习4、求斜边长17厘米、一条直角边长15厘米的直角三角形的面积。巩固练习5、如图,所有的四边形都是正方形,所有的三角形都是直角三角形,请在图中找出若干个图形,使它们的面积之和恰好等于最大的正方形面积,尝试给出两种以上的方案。ACDBEFG巩固练习6、如图,求等腰△ABC的面积。CBA5cm5cm6cmD课堂小结1、勾股定理:(1)文字语言:直角三角形两直角边的平方和等于斜边的平方。ABCabc(2)符号语言:90C222cba(已知)(勾股定理)课堂小结2、验证“勾股定理”的方法:(1)测量法(2)数格子法3、“勾股定理”的应用:已知直角三角形两边,求第三边。