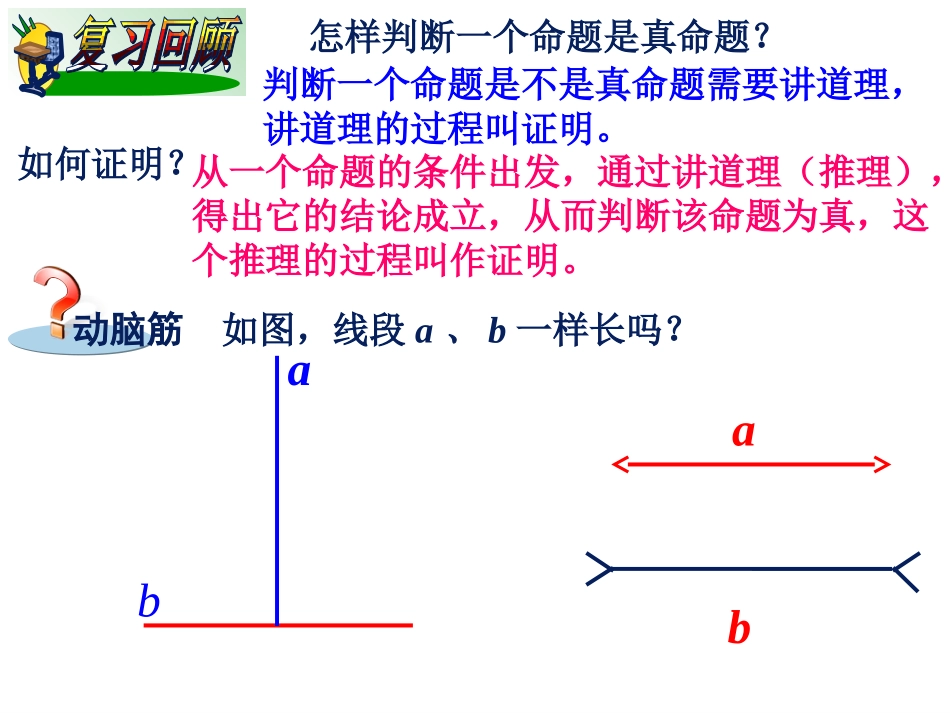
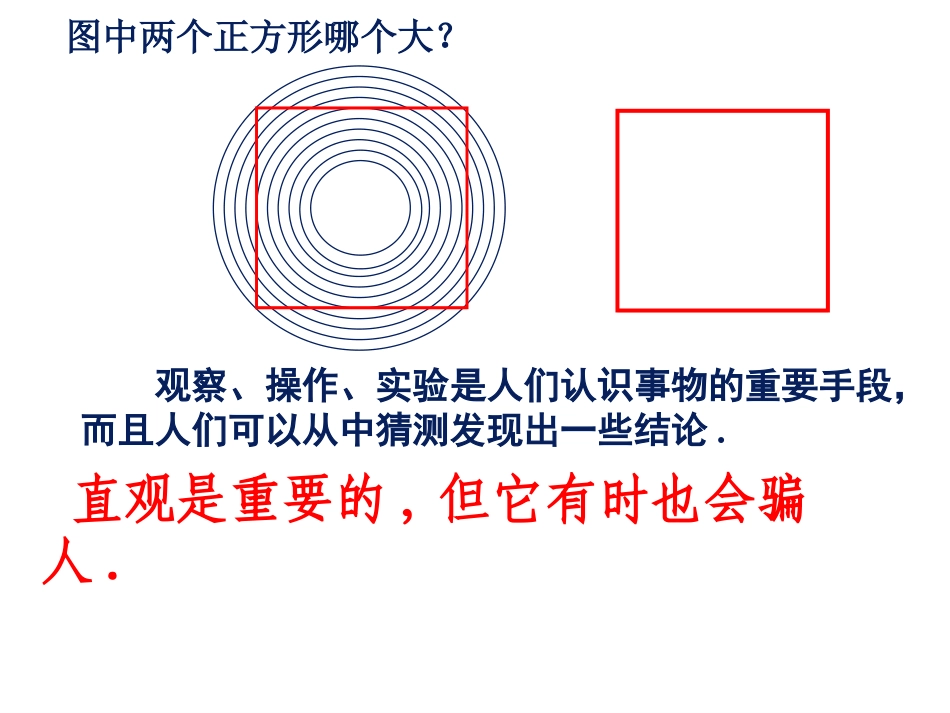
湘教版SHUXUE八年级上本节内容2.2abab动脑筋判断一个命题是不是真命题需要讲道理,讲道理的过程叫证明。如何证明?从一个命题的条件出发,通过讲道理(推理),得出它的结论成立,从而判断该命题为真,这个推理的过程叫作证明。怎样判断一个命题是真命题?如图,线段a、b一样长吗?图中两个正方形哪个大?观察、操作、实验是人们认识事物的重要手段,而且人们可以从中猜测发现出一些结论.直观是重要的,但它有时也会骗人.做一做采用剪拼或度量的方法,猜测“三角形的外角和”等于多少度.从剪拼或度量可以猜测三角形的三个外角之和等于360°,但是剪拼时难以真正拼成一个周角,只是接近周角;分别度量这三个角后再相加,结果可能接近360°,但不能很准确地都得360°.另外,由于不同形状的三角形有无数个,我们也不可能用剪拼或度量的方法来一一验证,因此,我们只能猜测任何一个三角形的外角和都为360°.此时猜测出的命题仅仅是一种猜想,未必都是真命题.要确定这个命题是真命题,还需要通过推理的方法加以证明.第一步:根据题意,画出图形;“证明命题三角形的外角和为360°”是真命题.动脑筋第二步:结合图形,写出已知求证;已知:∠BAF,∠CBD和∠ACE分别是△ABC的三个外角.求证:∠BAF+∠CBD+∠ACE=360°.第三步:写出证明过程,并且步步有依据。证明:如图, ∠BAF=2+3∠∠,∴∠BAF+∠CBD+∠ACE=2(1+2+3∠∠∠)(等式的性质).∠CBD=1+3∠∠,∠ACE=1+2∠∠(三角形外角定理), ∠1+2+3=180°∠∠(三角形内角和定理),∴∠BAF+∠CBD+∠ACE=2×180°=360°.经过刚才三站的“证明”之旅,你能说出完整的几何命题证明需要哪几个步骤吗?(1)根据题意,画出图形。(2)结合图形,写出已知求证(3)写出证明过程,并且步步有依据。结论依据(定义)(定理)(推论)(基本事实)(真命题)条件结论数学上证明一个命题时,通常从命题的条件出发,运用定义、基本事实以及已经证明了的定理和推论,通过一步步的推理,最后证实这个命题的结论成立.证明的每一步都必须要有根据.推理例1已知:如图,在△ABC中,∠B=∠C,点D在线段BA的延长线上,射线AE平分∠DAC.求证:AE∥BC.举例证明: ∠DAC=∠B+∠C(三角形外角定理),∠B=∠C(已知),∴∠DAC=2∠B(等式的性质).又 AE平分∠DAC(已知),∴∠DAC=2∠DAE(角平分线的定义)∴∠DAE=∠B(等量代换).∴AE∥BC(同位角相等,两直线平行)例2已知:∠A,∠B,∠C是△ABC的内角.求证:∠A,∠B,∠C中至少有一个角大于或等于60°.分析这个命题的结论是“至少有一个”,也就是说可能出现“有一个”、“有两个”、“有三个”这三种情况.如果直接来证明,将很繁琐,因此,我们将从另外一个角度来证明.证明假设∠A,∠B,∠C中没有一个角大于或等于60°即∠A<60°,∠B<60°,∠C<60°,则∠A+∠B+∠C<180°.这与“三角形的内角和等于180°”矛盾,所以假设不正确.因此,∠A,∠B,∠C中至少有一个角大于或等于60°.像这样,当直接证明一个命题为真有困难时,我们可以先假设命题不成立,然后利用命题的条件或有关的结论,通过推理导出矛盾,从而得出假设不成立,即所证明的命题正确,这种证明方法称为反证法.反证法是一种间接证明的方法,其基本的思路可归结为“否定结论,导出矛盾,肯定结论”.反证法的步骤:假设结论的反面成立→逻辑推理得出矛盾→肯定原结论正确结论(1).证明命题:一个角的两边分别平行于另一个角的两边,且方向相同,则这两个角相等。C'B'A'CBA已知:如图,AB∥A’B’,BC∥B’C’.求证:∠B=∠B’证明: AB∥A’B’()∴∠B’=∠α() BC∥B’C’()∴∠B=∠α()∴∠B=∠B’()已知两直线平行,同位角相等已知两直线平行,同位角相等等量代换练习1.在括号内填上理由.(2).已知:如图,∠A+∠B=180°.求证:∠C+∠D=180°.证明: ∠A+∠B=180°(已知),∴AD∥BC().∴∠C+∠D=180°().同旁内角互补,两直线平行两直线平行,同旁内角互补2.已知:如图,直线AB,CD被直线MN所截,∠1=2.∠求证:∠2=3∠,∠3+4=180°.∠证明: ∠1=2∠,∴∠2=3∠(两直线平行,内错角相等)∠3+4=180°∠(两直线平行...