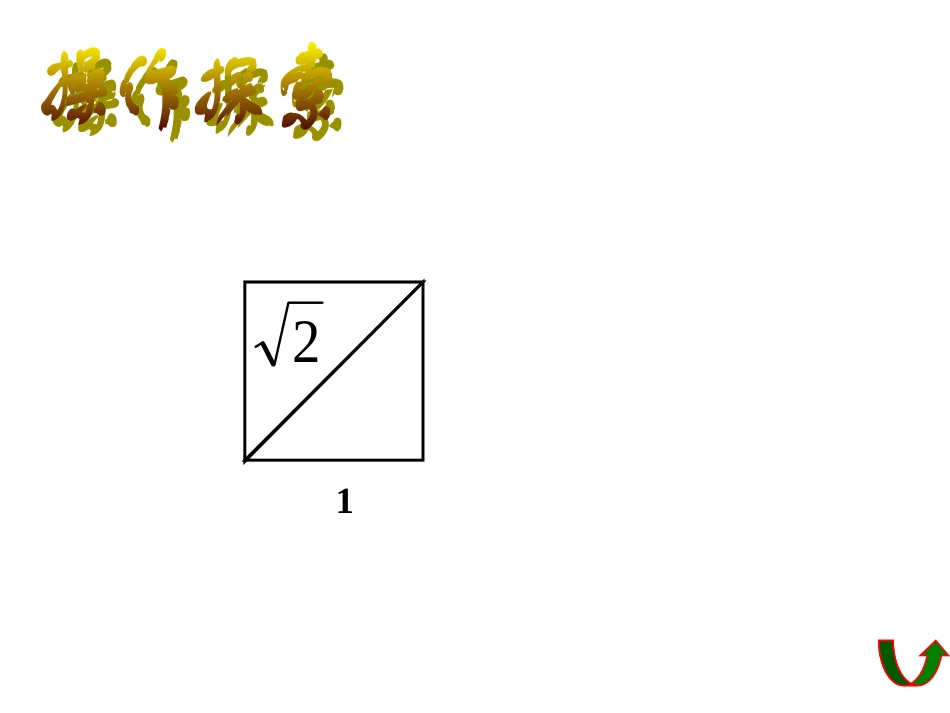
12学习目标1、会算术平方根、平方根、立方根的概念、性质和运算;2、会梳理和归纳本章内容,把本章的学习内容纳入自己的知识体系。1、回顾算术平方根、平方根、立方根概念及性质(1)算术平方根的定义:一般地,如果一个正数x的平方等于a,即=a,那么这个正数x叫做a的算术平方根。a的算术平方根记为,读作“根号a”,a叫做被开方数。x2特殊:0的算术平方根是0。00记作:一、知识储备一般地,如果一个数的平方等于a,那么这个数就叫做a的平方根(或二次方根).这就是说,如果x2=a,那么x就叫做a的平方根.a的平方根记为±a2.平方根的定义:3.立方根的定义:一般地,如果一个数的立方等于a,那么这个数就叫做a的立方根,也叫做a的三次方根.记作.3a其中a是被开方数,3是根指数,符号“”读做“三次根号”.3算术平方根、平方根、立方根概念及性质你知道算术平方根、平方根、立方根联系和区别吗?算术平方根算术平方根平方根平方根立方根立方根表示方法a的取值性质a3aa≥0a是任何数开方a≥0a正数0负数正数(一个)0没有互为相反数(两个)0没有正数(一个)0负数(一个)求一个数的平方根的运算叫开平方求一个数的立方根的运算叫开立方≠是本身0,100,1,-12a2a33a33a=a0a00aa)0(aaaaa33aa0a为任何数a为任何数a为任何数a1.求下列各数的算术平方根:(1)0.04;(2)1;(3)56;(4)(-3)2;(5)49643.求下列各数的立方根:(1)121;(2)16;(3)0;(4)(-3)2;(5)942.求下列各数的平方根:(1)-0.008;(2)43;(3)-64;(4)(-3)3;(5)2784.求下列各式的值:16.0)1(31(4)169)2(925)3(327125)5(求根也好,求值也好,关键要弄清它是什么意思,然后可以选择定义和性质来求.214.3-()6()π不要搞错了是8的平方根的平方根是64的值是64的平方根是9的立方根是6464±883-42、实数的概念、分类和性质1、无理数的概念:2、实数的概念:有理数和无理数统称为实数3、实数的分类:无限不循环小数叫无理数实数有理数无理数分数整数正整数0负整数正分数负分数自然数正无理数负无理数无限不循环小数有限小数及无限循环小数一般有三种情况、)1(开不尽的数”“”“23,、00010100100010.0)3(类似于、(1)按定义分:有理数集合:{,};1、把下列各数填在相应的大括号内:,1,75,,14.3,0,333.3,3,643.1010010001.2整数集合:{……};分数集合:{……};无理数集合:{……}。-1,0,364-1,3.14,0,,75364π,2.1010010001…,375,333.3,333.33.14,4122、把下列各数分别填入相应的集合内:、把下列各数分别填入相应的集合内:22、把下列各数分别填入相应的集合内:、把下列各数分别填入相应的集合内:,23,7,,25,23,5,83,94,03737737773.0有理数集合有理数集合有理数集合有理数集合无理数集合无理数集合无理数集合无理数集合,83,41,25,94,0,23,7,,2,3,53737737773.001-1√2如图是两个边长1的正方形拼成的长方形,其面积是2.现剪下两个角重新拼成一个正方形,新正方形的边长是_____√2√22√2下图数轴中,正方形的对角线长为____,以原点为圆心,对角线长为√2半径画弧截得一点,该点与原点的距离是____,√2该点表示的数是____.√2√2-在数轴上作出对应的点。在数轴上作出对应的点。5-2-2-1-10011221552、实数与数轴上的点是一一对应关系.33、、在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。(1)a是一个实数,它的相反数为,绝对值为;(2)如果a0,那么它的倒数为.aaa15、在进行实数的运算时,有理数的运算法则实数的运算时,有理数的运算法则及运算性质同样适用。及运算性质同样适用。实数的有关概念和性质4、实数的大小比较方法有:利用数轴比较、利用绝对值比较、求平方比较、求差比较等方法。二、课堂检测二、课堂检测1、判断下列说法是否正确:1.实数不是有理数就是无理数。()2.无限小数都是无理数。()3.无理数都是无限小数。()4.带根号的数都是无理数。()5.两个无理数之积一定是无理数。()6.所有的有理数都可以在数...