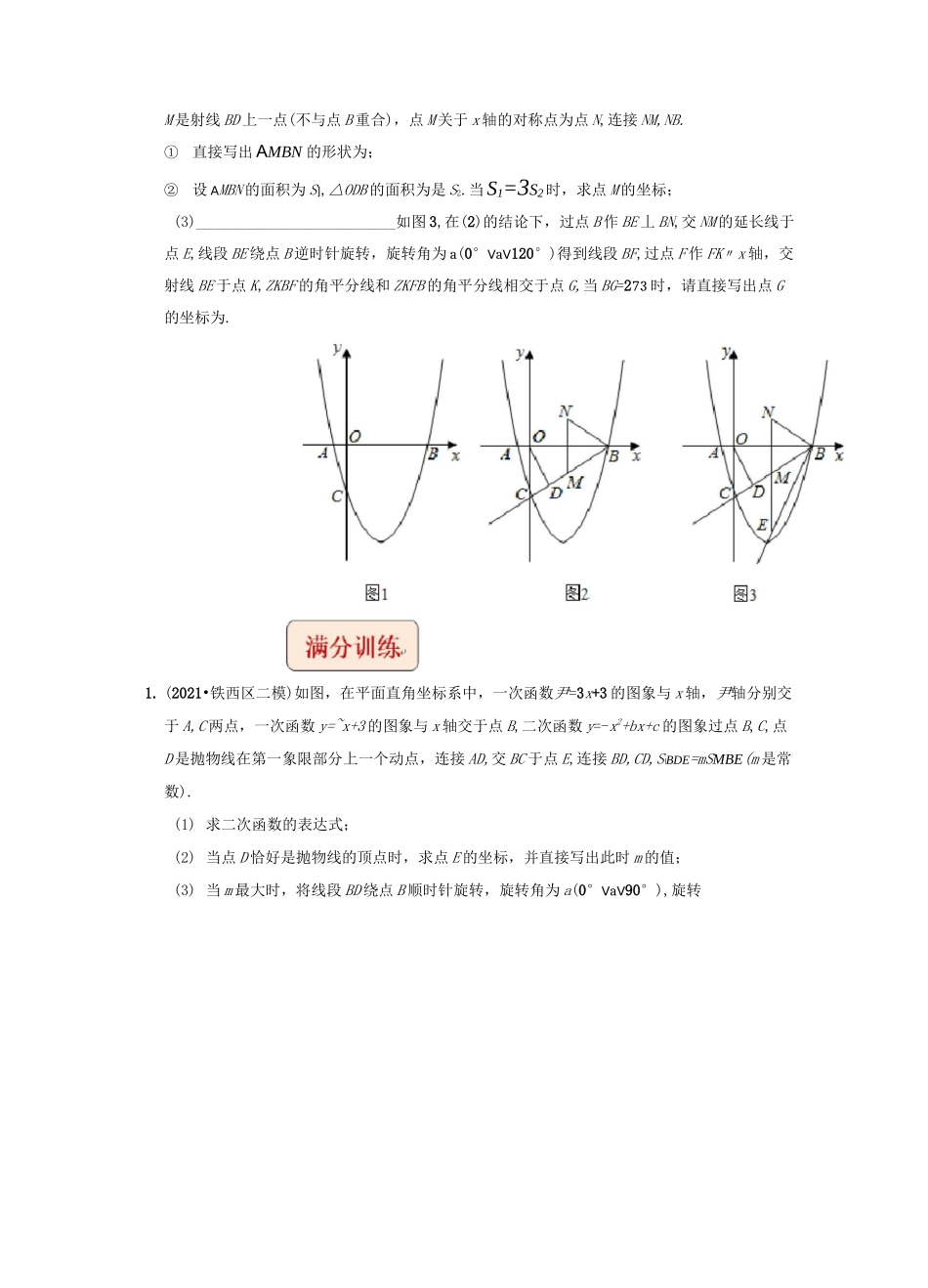
挑战2022年中考数学压轴题之学霸秘笈大揭秘专题16二次函数与几何变换综合问题典例剖析+|【例1】(2021•绵阳)如图,二次函数y=-x2-2x+4-^2的图象与一次函数y=-2x的图象交于点A、B(点B在右侧),与y轴交于点C,点A的横坐标恰好为a.动点P、Q同时从原点O出发,沿射线OB分别以每秒.亍和2.E个单位长度运动,经过t秒后,以PQ为对角线作矩形PMQN,且矩形四边与坐标轴平行.(1)求a的值及t=1秒时点P的坐标;(2)当矩形PMQN与抛物线有公共点时,求时间t的取值范围;(3)在位于x轴上方的抛物线图象上任取一点人,作关于原点(0,0)的对称点为R',当点M恰在抛物线上时,求R'M长度的最小值,并求此时点R的坐标.【例2】(2021•德州)小刚在用描点法画抛物线C]:y=ax2+bx+c时,列出了下面的表格:x…01234…y…36763…(1)________________________________________________________请根据表格中的信息,写出抛物线C1的一条性质:;(2)求抛物线C1的解析式;(3)将抛物线C1先向下平移3个单位长度,再向左平移4个单位长度,得到新的抛物线C2;①若直线y=x+b与两抛物线C1,C2共有两个公共点,求b的取值范围;■Lu②抛物线C2的顶点为A,与x轴交点为点B,C(点B在点C左侧),点P(不与点A重合)在第二象限内,且为C2上任意一点,过点P作PD丄x轴,垂足为D,直线AP交y轴于点Q,连接AB,DQ.求证:AB〃DQ.【例3】(2021•兰州)如图1,二次函数y=a&+3)4)图象交坐标轴于点A,B(0,-2),点P为x轴上一动点.(1)求二次函数y=a(x+3)(x-4)的表达式;(2)过点P作PQ丄x轴分别交线段AB,抛物线于点Q,C,连接AC.当OP=1时,求AACQ的面积;(3)如图2,将线段PB绕点P逆时针旋转90°得到线段PD.当点D在抛物线上时,求点D的坐标.【例4】(2021•天津二模)已知抛物线C:y=-x2+x+2与x轴交于点A,B(点A在点B左狈D,与y轴交于点K,顶点为D.(I)求点A,B,K,D的坐标;(II)若向下平移抛物线C,使顶点D落在x轴上,抛物线C上的点P平移后的对应点为P',若OP=OP,求点P的坐标;(III)点E(-2,n)在抛物线C上,则在抛物线C上是否存在一点Q,使AOBE的面积是ABEK面积的一半,若存在,求满足条件的点Q的坐标;若不存在,说明理由.1【例5】(2020•沈阳)如图1,在平面直角坐标系中,O是坐标原点,抛物线y=2x2+bx+c经过点B(6,0)和点C(0,-3).(1)求抛物线的表达式;(2)如图2,线段OC绕原点O逆时针旋转30°得到线段OD.过点B作射线BD,点M是射线BD上一点(不与点B重合),点M关于x轴的对称点为点N,连接NM,NB.①直接写出AMBN的形状为;②设AMBN的面积为S],△ODB的面积为是S2.当S1=3S2时,求点M的坐标;(3)___________________________如图3,在(2)的结论下,过点B作BE丄BN,交NM的延长线于点E,线段BE绕点B逆时针旋转,旋转角为a(0°VaV120°)得到线段BF,过点F作FK〃x轴,交射线BE于点K,ZKBF的角平分线和ZKFB的角平分线相交于点G,当BG=273时,请直接写出点G的坐标为.1.(2021•铁西区二模)如图,在平面直角坐标系中,一次函数尹=3x+3的图象与x轴,尹轴分别交于A,C两点,一次函数y=~x+3的图象与x轴交于点B,二次函数y=-x2+bx+c的图象过点B,C,点D是抛物线在第一象限部分上一个动点,连接AD,交BC于点E,连接BD,CD,S\BDE=mSMBE(m是常数).(1)求二次函数的表达式;(2)当点D恰好是抛物线的顶点时,求点E的坐标,并直接写出此时m的值;(3)当m最大时,将线段BD绕点B顺时针旋转,旋转角为a(0°VaV90°),旋转2.(2021•皇姑区一模)如图,在平面直角坐标系中,抛物线y=ax2+bx+4交y轴于点A,交x轴于点B(-6,0)和点C(2,0),点Q在第一象限的抛物线上,连接AB、AQ、BQ,BQ与y轴于点N.(1)求抛物线表达式;(2)当AAB。的面积等于7时,设点Q的横坐标为m,求m的值;(3)在(2)的条件下,点M在x轴上,点E在平面内,若△BME95AOM,四边形ANEM是平行四边形;①直接写出点E的坐标;②设射线AM与BN相交于点P,交BE于点H,将AEPH绕点B旋转一周,旋转后的三角形记为△BP1H1,直接写出BP1+.2OH1的最小值.备用图3.(2021•大东区二模)如图,抛物线y=ax2+bx+6与x轴交于点B(-4,0),C(2,0),与y轴交于点A,在抛物线上有一动点P,连接AP,BP,AB,CP.(1)求该抛物线的函数表达式;(2)若P点在第二象限的抛物线上,当AABP的面积是鲁时,求ABCP的面积;(3)点D是线...