第3课时相似三角形的判定定理2VIP免费

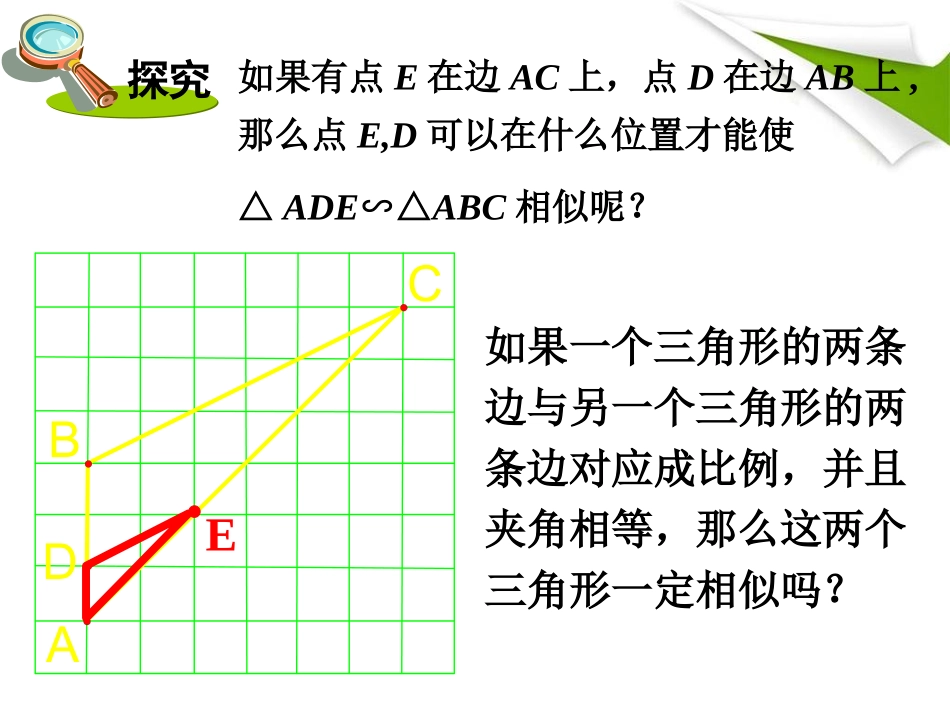
第3课时相似三角形的判定定理23.4.1相似三角形的判定DCBA如果有点E在边AC上，点D在边AB上,那么点E,D可以在什么位置才能使△ADE∽△ABC相似呢？如果一个三角形的两条边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形一定相似吗？E探究结论相似三角形的判定定理2如果一个三角形的两条边和另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似.相似三角形的判定定理2如果一个三角形的两条边和另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似.ABCABCABABACACAA''BB''AA''CC''如如果果∠A=∠A'，那么ΔABCΔ∽A'B'C'想一想：如果对应相等的角不是两条对应边的夹角，那么两个三角形是否相似呢？ABCDEF动脑筋例1已知在Rt△ABC与Rt△中，∠C=∠C′=90°，AC=3cm，BC=2cm，=4.2cm，=2.8cm.求证：△∽△ABC.ABCACBCABC证明：557790，∵,,ACBC==ACBCC=C=∴△ABC.∽△ABC举例△ABC为锐角三角形，BD、CE为高.求证：△ADE∽△ABC.1O23ABCDE举例例2证明：∵BD⊥AC，CE⊥AB，∴∠ABD+∠A=90°，∠ACE+∠A=90°.∴∠ABD=∠ACE.又∵∠A=∠A，∴△ABD∽△ACE.∴∵∠A=∠A，∴△ADE∽△ABC..ADAB=AEAC动脑筋如图，在△ABC与△DEF中，∠B=∠E=40°，AB=4.2cm，AC=3cm，DE=2.1cm，DF=1.5cm.△ABC与△DEF有两边对应成比例吗？有一个角对应相等吗？这两个三角形相似吗？从上述例子你能得出什么结论？图3-21有两边对应成比例.有两边对应成比例.22ABACDEDF，，图中∠B=∠E，而∠A≠∠D，故这两个三角形不相似.图中∠B=∠E，而∠A≠∠D，故这两个三角形不相似.在两个三角形中，有两边对应成比例，如不是这两边的夹角相等，则这两个三角形不相似.在两个三角形中，有两边对应成比例，如不是这两边的夹角相等，则这两个三角形不相似.22ABACDEDF，，有两边对应成比例.图中∠B=∠E，而∠A≠∠D，故这两个三角形不相似.在两个三角形中，有两边对应成比例，如不是这两边的夹角相等，则这两个三角形不相似.1.如图，D是△ABC一边BC上一点，连接AD,使△ABC∽△DBA的条件是（）A.AC:BC=AD:BDB.AC:BC=AB:ADC.AB2=CD·BCD.AB2=BD·BCDACBD练习2.已知在Rt△ABC与Rt△中，∠A=∠A′=90°，AB=6cm，AC=4.8cm，=5cm，=3cm.求证：△∽△ABC.ABCABBCABC证明：64.8655490,.,∵ABAC===ABACC=C=∴△ABC∽△.ABC练习3.在正方形ABCD中，E为AD上的中点,F是AB的四分一等分点，连结EF、EC；△AEF与△DCE是否相似?说明理由.ABCDFE1.2EABFAFEDAEEC解：为的中点，为AB的四等分点，四边形ABCD为正方形，A=D.△AEF∽△DEC.练习