《132函数的奇偶性（1）》课件VIP免费

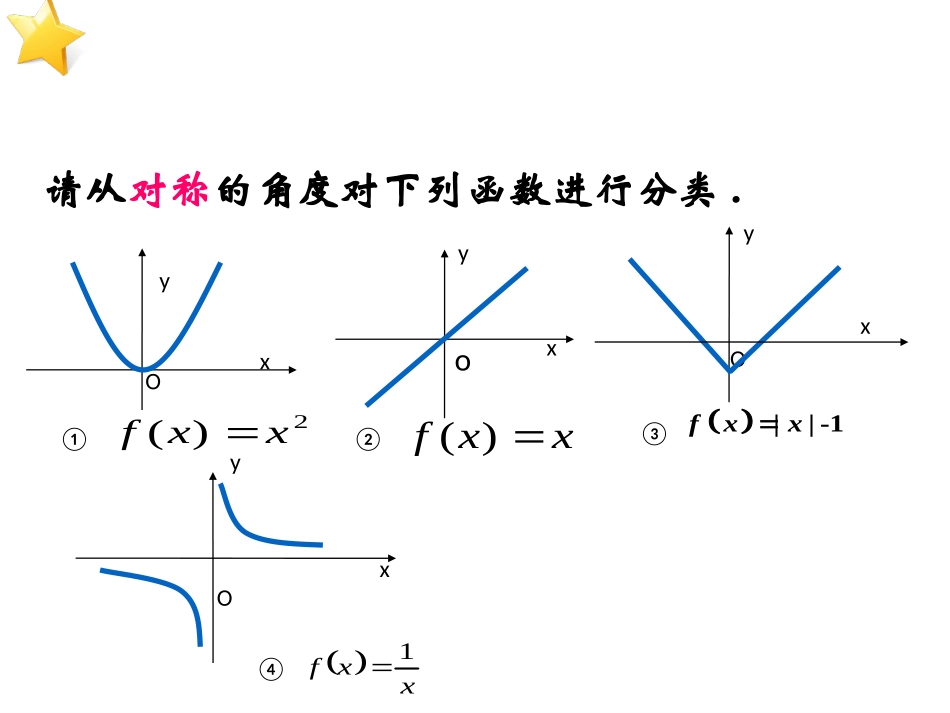
轴对称图形中心对称图形沿着一条直线对折后的两部分能够完全重合后的图形叫轴对称图形；绕某点旋转180度后的图形能和原图形完全重合的图形叫中心对称图形；请从对称的角度对下列函数进行分类.③Oxy①2)(xxf②xyxxf)(④Oxyoxxf1Oyx-1fx|x|Oxy①2)(xxf函函函函函函函函函函函函yy函函函函函函函函函函函函函函函函函函函函函函函函函函函函函函函函Oyx-1fx|x|③Oxy①2)(xxf③Oyx-1fx|x|x-3-2-10123f(x)=x2x-3-2-10123f(x)=|x|-14101491209-1012填写下列表格思考：从上面的表格，你能看出当自变量的值互为相反数时，函数值有什么关系？定义：定义：如果对于函数如果对于函数f(x)f(x)定义域内的任意一个定义域内的任意一个xx，都有，都有f(-x)=f(x)f(-x)=f(x)成立，那么称函数成立，那么称函数f(x)f(x)为为偶函数偶函数..证明：证明：f(x)=xf(x)=x22为为偶函数偶函数..RRx证明：定义域为，任取22fxxxfxfx因此是偶函数②xyxxf)(o④Oxxxf1函函函函函函函函函函函函函函函函函函函函函函函函函函函函函函函函函函函函函函函函函函函函函函x-3-2-10123f(x)=xx-3-2-10123f(x)=1/x-2-10123-1/2-1/3-1-3/11/21/3填写下列表格思考：从上面的表格，你能看出当自变量的值互为相反数时，函数值有什么关系？xyxxf)(o④Oxxxf1定义：定义：如果对于函数如果对于函数f(x)f(x)定义域内的任意一个定义域内的任意一个xx，都有，都有f(-x)=-f(x)f(-x)=-f(x)成立，那么称函数成立，那么称函数f(x)f(x)为为奇函奇函数数..证明：证明：f(x)=xf(x)=x33为奇函数为奇函数..RRx证明：定义域为，任取33--fxxxfxfx因此是奇函数f(x)关于原点对称函函函函函函函函函x，有f(-x)=-f(x)f(x)为奇函数f(x)关于y轴对称函函函函函函函函函x，有f(-x)=f(x)f(x)为偶函数2f(x)x函数是奇函数还是偶函数？2-12f(x)xx函数,，是奇函数还是偶函数？Oxy2f(x)x]2,1[,)(2xxxf-12Oxy2,2)(2xxxf，是奇函数还是偶函数？，函数2,2)(2xxxf-222)(xxf是什么原因导致上述三种情况函数的奇偶性不同？函函函函函函函函函函函函函函函函函函函函函函函函函函OxyOxy1函函函函函函函函函函函函函函函函函函函函函函函函函函函函例1、判断下列函数的奇偶性：xxxfxxfxxfxxf1)()4(1)()3()()2()()1(2544.下结论.判断奇偶性的方法：1.定义法2.图像法3.性质法：在公共的定义域内，若是奇函数，是奇函数，则)(xf)(xg为)()(xgxf奇为)()(xgxf奇为)()(xgxf偶在公共的定义域内若是偶函数，是偶函数，则)(xf)(xg为)()(xgxf偶偶偶在公共的定义域内，若是奇函数，是偶函数，则)(xf)(xg为)()(xgxf奇函数图象关于y轴对称.从几何上看：从几何上看：从代数上看：从代数上看：从几何上看：从几何上看：从代数上看：从代数上看：函数图象关于原点对称.xy0xy0fxgx