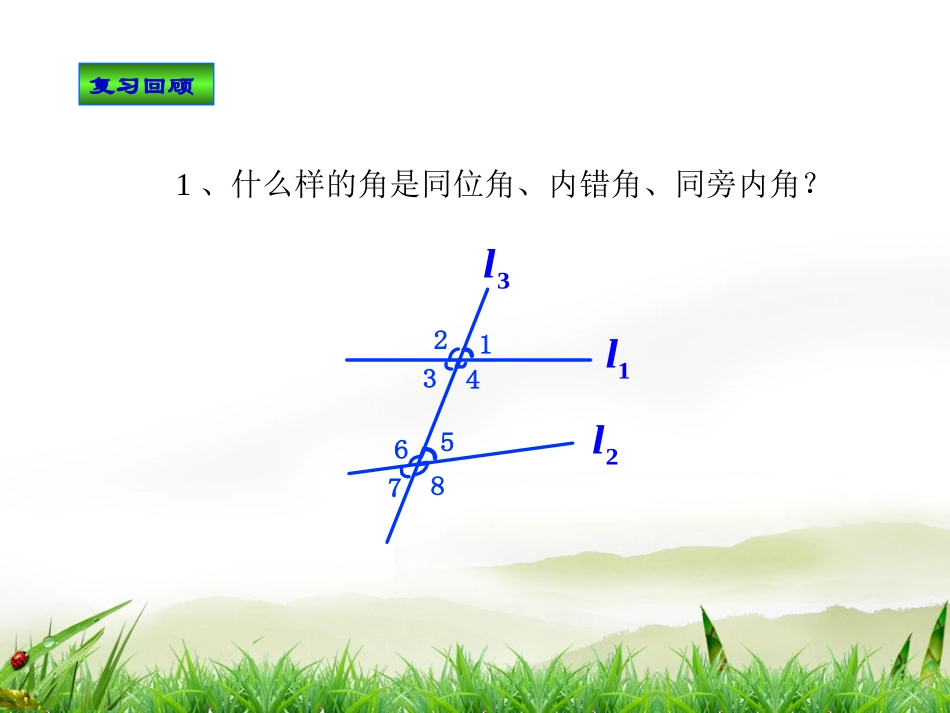
5.3.1平行线的性质(一)嘉鱼县实验中学:龚小明2016.03.09复习回顾1、什么样的角是同位角、内错角、同旁内角?3l1l2l12345678复习回顾2、平行公理及其推论是什么?平行公理:经过直线外一点,有且只有一条直线与这条直线平行。推论:如果两条直线都和第三条直线平行,那么这两条直线也互相平行。根据右图,填空:①如果∠1=∠C,那么__∥__()②如果∠1=∠B那么__∥__()③如果∠2+∠B=180°,那么__∥__()EACDB1234ABCDECBD同位角相等,两直线平行内错角相等,两直线平行ECBD同旁内角互补,两直线平行复习回顾复习回顾3、平行线的判定方法有哪些?同位角相等,两直线平行。内错角相等,两直线平行。同旁内角互补,两直线平行。4、这些判定方法先知道什么,后知道什么?复习回顾同位角相等,内错角相等,同旁内角互补,两直线平行。新课学习如果两条直线平行,那么这两条平行线被第三条直线所截而成的同位角会有什么关系呢?abc21平行线的第一个性质(公理)两条平行线被第三条直线所截,同位角相等。简称:两直线平行,同位角相等。新课学习如图:已知ab∥,那么∠3与∠2是什么关系?∵a∥b∴∠1=∠2又∵∠1=∠3∴∠3=∠2(等量代换)(已知)(两直线平行,同位角相等)(对顶角相等)平行线的性质2:两条平行线被第三条直线所截,内错角相等。简称:两直线平行,内错角相等。123abc新课学习解:如图:已知ab∥,那么∠2与∠4会有什么关系呢?∵ab∥∴∠1=2∠又∵∠1+4=180∠o∴∠2+4=180∠o(等量代换)(已知)(两直线平行,同位角相等)(邻补角定义)平行线的性质3两条平行线被第三条直线所截,同旁内角互补。简称:两直线平行,同旁内角互补。1234abc新课学习解:新课学习平行线的三条性质:平行线的性质1:两直线平行,同位角相等。平行线的性质2:两直线平行,内错角相等。平行线的性质3:两直线平行,同旁内角互补。巩固练习4321ACBDE例1:已知AB//CD,∠1=110°,∠2,∠3,∠4的度数。例2:如图,由AB//CD,可以得到()A.∠1=∠2B.∠2=∠3C.∠1=∠4D.∠3=∠4BDAC1234C巩固练习你能区别平行线的判定与性质吗?你能区别平行线的判定与性质吗?同位角相等内错角相等同旁内角互补两直线平行。判定性质新课学习1、如图,是有梯形上底的一部分,已经量得∠A=115o,∠D=100o,梯形另外两个角各是多少度?解:∵ADBC∥(梯形定义)∴∠A+B=180∠o∠C=180o-100o=80o答:梯形的另外两个角分别是65o和80o。(两直线平行,同旁内角互补)(等式性质1)DCBA于是∠B=180o-115o=65o∠D+C=180∠o(两直线平行,同旁内角互补)(等式性质1)当堂训练2、如图,已知D是AB上一点,E是AC上一点,∠ADE=60o,∠B=60o,∠AED=40o(1)DE和BC平行吗?为什么?(2)∠C是多少度?为什么?EDCBA当堂训练1.平行线的三条性质。2.平行线性质和判定的区别。两条直线被第三条直线所截得的同位角、内错角都相等吗?同旁内角都互补吗?课堂小结思考?课本:第87页,第9题、第10题作业布置1、如图,已知AB//CD,∠A=∠C,试说明∠E=∠FADECBF补充作业补充作业154°ABFDCE154°ABFDCE2、已知AB//EF//CD,∠ABC=46°,∠CEF=154°,则∠BCE等于()A23°B16°C20°D26°补充作业3、已知AB∥CD,直线EF分别交AB,CD于E,F,EG平分∠BEF,若∠1=72°,则∠2的度数GFEDCBA12MN