一元二次方程的解法复习课1VIP免费

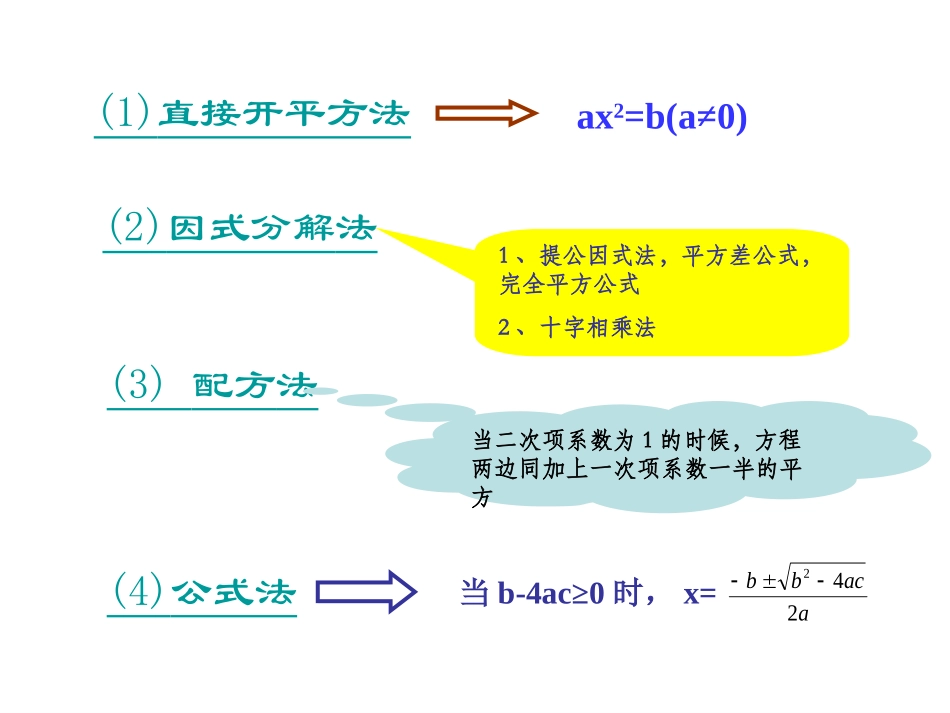
一元二次方程的解法腾达中学：陈言明2008.9.25(1)直接开平方法ax2=b(a≠0)(2)因式分解法1、提公因式法，平方差公式，完全平方公式2、十字相乘法(3)配方法当二次项系数为1的时候，方程两边同加上一次项系数一半的平方(4)公式法当b-4ac≥0时，x=aacbb242一直接开平方法依据：平方根的意义，即如果x2=a,那么x=.a这种方法称为直接开平方法。解题步骤：1，将一元二次方程常数项移到方程的一边。2，利用平方根的意义，两边同时开平方。3，得到形如：x=.a的一元一次方程。4，写出方程的解x1=?,x2=?1、（3x-2）²-49=02、（3x-4）²=（4x-3）²解：移项，得：（3x-2）²=49两边开平方，得：3x-2=±7所以：x=所以x1=3，x2=-35372解：两边开平方，得：3x-4=±（4x-3）3x-4=4x-3或3x-4=-4x+3-x=1或7x=7x=-1，x=1例题讲解二因式分解法)2(5)2(3)1(xxx)2(5)2(3xxx解：移项，得(32)6(32)0xxx1提公因式法=0（2）解：提公因式得：(32)(6)0xx32060xx或123x26x提公因式得(35)(2)0xx35020xx或153x22x2平方差公式与完全平方公式220xa()()0xaxa2220xaxa形如运用平方差公式得：2()0xa12xxa12xxa00xaxa或1xa2xa形如的式子运用完全平方公式得：或例题讲解例1解下列方程（1）216(2)90x29(2)16x324x解：原方程变形为：154x2114x(2)10xx2210xx2(1)0x121xx直接开平方得：（2）解：原方程变形为：3十字相乘法1二次项系数为1的情况：将一元二次方程常数项进行分解成两个数(式)p,q的乘积的形式，且p+q=一次项系数。步骤：2二次项系数不为1的情况：将二次项系数分成两个数（式）a,b的乘积的形式，常数项分解成p,q的乘积的形式，且aq+bp=一次项系数。PQABPQ分解结果为（x+p）(x+q)=0分解结果为（ax+p）(bx+q)=01106)23()2(2xx0)2)(3(xx解：原方程变形为,0203xx或.2,321xx例题讲解用十字相乘法解下列方程18)2)(5)(1(xx解：整理原方程，得x2－３x－28=0(x－7)(x+4)=0x－7=0或x+4=0x1=7,x2=-402222baaxxx的方程解关于.,21baxbax0)]()][([baxbax解：0)(0)(baxbax或11)()(baba例题讲解三配方法我们通过配成完全平方式的方法,得到了一元二次方程的根,这种解一元二次方程的方法称为配方法平方根的意义:完全平方式:式子a2±2ab+b2叫完全平方式,且a2±2ab+b2=(a±b)2.如果x2=a,那么x=.a用配方法解一元二次方程的方法的助手:用配方法解一元二次方程：2x2-9x+8=0.0429:2xx解.41749x.4494929222xx.1617492x.41749x.4292xx1.化1:把二次项系数化为1;3.配方:方程两边都加上一次项系数绝对值一半的平方;4.变形:方程左边分解因式,右边合并同类;5.开方:两边开平方;6.求解:解一元一次方程;7.定解:写出原方程的解.2.移项:把常数项移到方程的右边;.4179;417921xx例题讲解例1.用配方法解下列方程x2+6x-7=0762xx：解97962xx1632x43x7121xx例题讲解例2.用配方法解下列方程2x2+8x-5=02542xx：解425442xx21322x2262x2226222621xx四公式法一般地,对于一元二次方程ax2+bx+c=0(a≠0).04.2422acbaacbbx上面这个式子称为一元二次方程的求根公式.用求根公式解一元二次方程的方法称为公式法:,042它的根是时当acb提示:用公式法解一元二次方程的前提是:1.必需是一元二次方程。2.b2-4ac≥0.例1用公式法解方程2x2-9x+8=0.8,9,2:cba解.417922179242aacbbx1.变形:化已知方程为一般形式;3.计算:b2-4ac的值;4.代入:把有关数值代入公式计算;5.定解:写出原方程的根.2.确定系数:用a,b,c写出各项系数;.0178249422acb.4179;417921xx例题讲解例2.用公式法解方程2x2+5x-3=0解: a=2b=5...