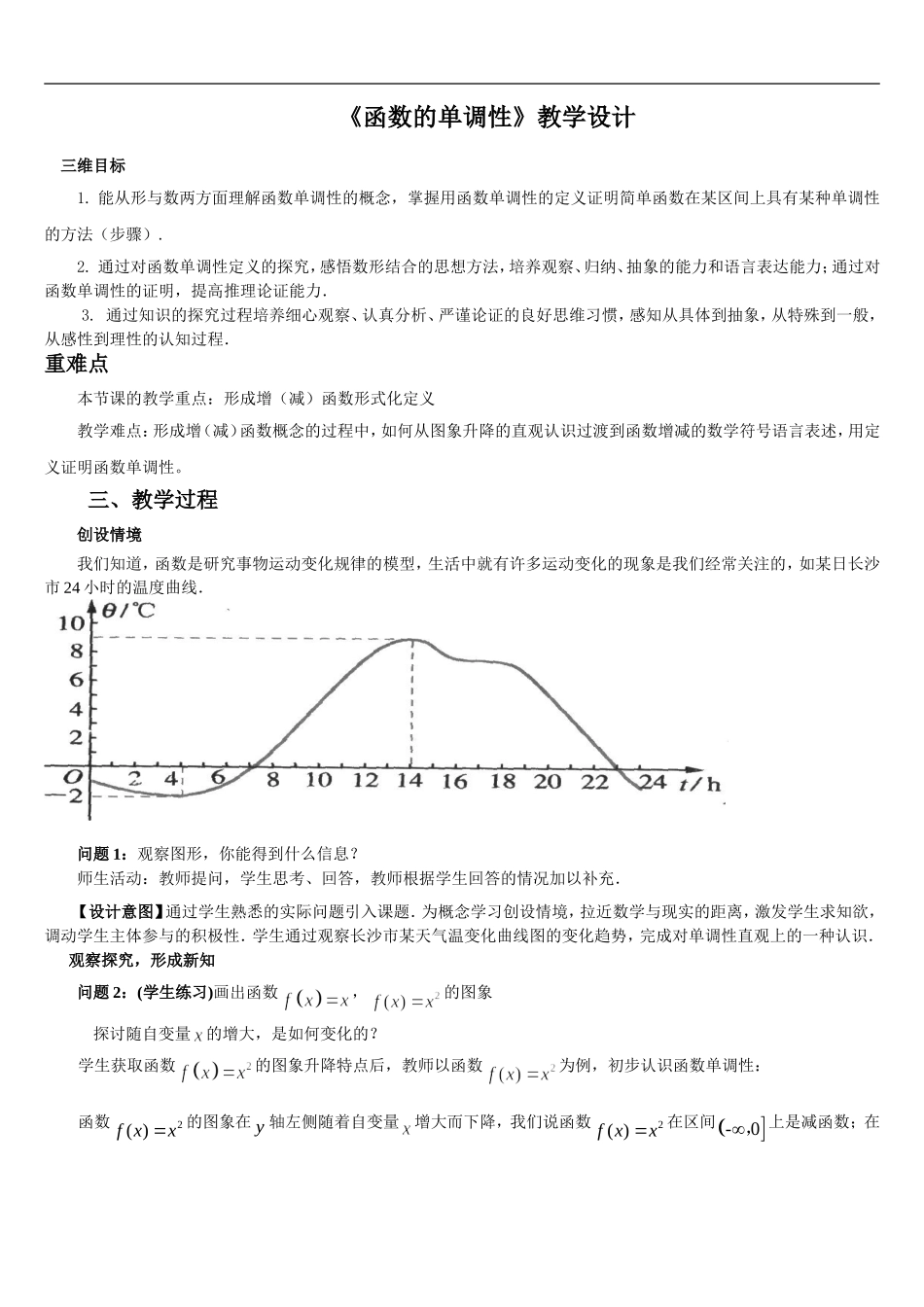
《函数的单调性》教学设计三维目标1.能从形与数两方面理解函数单调性的概念,掌握用函数单调性的定义证明简单函数在某区间上具有某种单调性的方法(步骤).2.通过对函数单调性定义的探究,感悟数形结合的思想方法,培养观察、归纳、抽象的能力和语言表达能力;通过对函数单调性的证明,提高推理论证能力.3.通过知识的探究过程培养细心观察、认真分析、严谨论证的良好思维习惯,感知从具体到抽象,从特殊到一般,从感性到理性的认知过程.重难点本节课的教学重点:形成增(减)函数形式化定义教学难点:形成增(减)函数概念的过程中,如何从图象升降的直观认识过渡到函数增减的数学符号语言表述,用定义证明函数单调性。三、教学过程创设情境我们知道,函数是研究事物运动变化规律的模型,生活中就有许多运动变化的现象是我们经常关注的,如某日长沙市24小时的温度曲线.问题1:观察图形,你能得到什么信息?师生活动:教师提问,学生思考、回答,教师根据学生回答的情况加以补充.【设计意图】通过学生熟悉的实际问题引入课题.为概念学习创设情境,拉近数学与现实的距离,激发学生求知欲,调动学生主体参与的积极性.学生通过观察长沙市某天气温变化曲线图的变化趋势,完成对单调性直观上的一种认识.观察探究,形成新知问题2:(学生练习)画出函数,的图象探讨随自变量的增大,是如何变化的?学生获取函数的图象升降特点后,教师以函数为例,初步认识函数单调性:函数2()fxx的图象在y轴左侧随着自变量增大而下降,我们说函数2()fxx在区间-0,上是减函数;在y轴右侧随着自变量增大上而升,就说函数2()fxx在区间0+,上是增函数.师生活动:教师引导,学生观察图象从左至右的变化情况,并回答问题.【设计意图】体会函数的图象是上升的,函数的图象在轴左侧是下降的,在轴右侧是上升的.以函数2()fxx的图象为例,通过函数的图象直观感知函数的单调性,初步认识函数单调性定义.探究一:用数学符号语言定义增函数.问题3:①函数的图象在轴右侧是上升的,如何用数学语言来描述这种“上升”?②观察表格,轴右侧自变量值与对应的函数值的变化规律是怎样的?教师提出问题①后,组织学生填写表格,观察图表…-012345678...师生活动:学生观察函数图象在轴右侧是上升的,提出函数在区间上随的增大而增大,在教师的帮助下,借助几何画板软件加以验证.【设计意图】观察函数的图象,用“在随的增大而增大”描述“图象在轴右侧是上升的”,进一步认识函数的单调性,从图形的刻画过渡到数量关系,即从图形语言的表述过渡到数学语言的表述.问题4:函数,你认为下面说法对吗?师生活动:在教师的引导下,学生解决以上问题。【设计意图】通过反例说明要取遍所有的数,明确“任意性”的要求.问题5:如何用数学符号语言描述函数在随的增大而增大?师生活动:学生在教师的引导下,总结:函数,在区间上任取值,当时,都有.就能说明函数在区间上随的增大而增大;函数是增函数.引导学生观察图象,进行验证,并通过作差比较,对函数在区间上当时,都有,给予证明.经历上述观察、猜想、分析、验证、证明的过程,得到结论:函数定义域为R,在上任意的的值,当时,都有.我们就说函数在区间上是增函数.【设计意图】结合图、表,学生在教师的引导,结合其初中的认知基础,学生在教师的引导下,用数学符号语言“函数,在区间上任取两个,当时,有”来描述“随着的增大而增大”,学生经历从直观到抽象,从图形语言到数学符号语言,进而理解增函数、减函数、单调区间概念的过程.问题6:对于一般的函数定义域为I,在区间D上,我们应当如何给增函数下定义?引导学生给增函数下定义:一般地,设函数的定义域为:如果对于定义域内的某个区间上的任意两个自变量的值,当时,都有,那么就说函数在区间上是增函数.师生活动:学生思考、发言,教师补充、板书.【设计意图】体现了对函数研究的一般方法:由特殊到一般的思想方法.问题7:类比增函数的定义,对于一般的函数,我们应当如何给减函数下定义?教师引导学生通过类比、观察、验证、交流后,得出减函数定义师生活动:小组讨论,代...