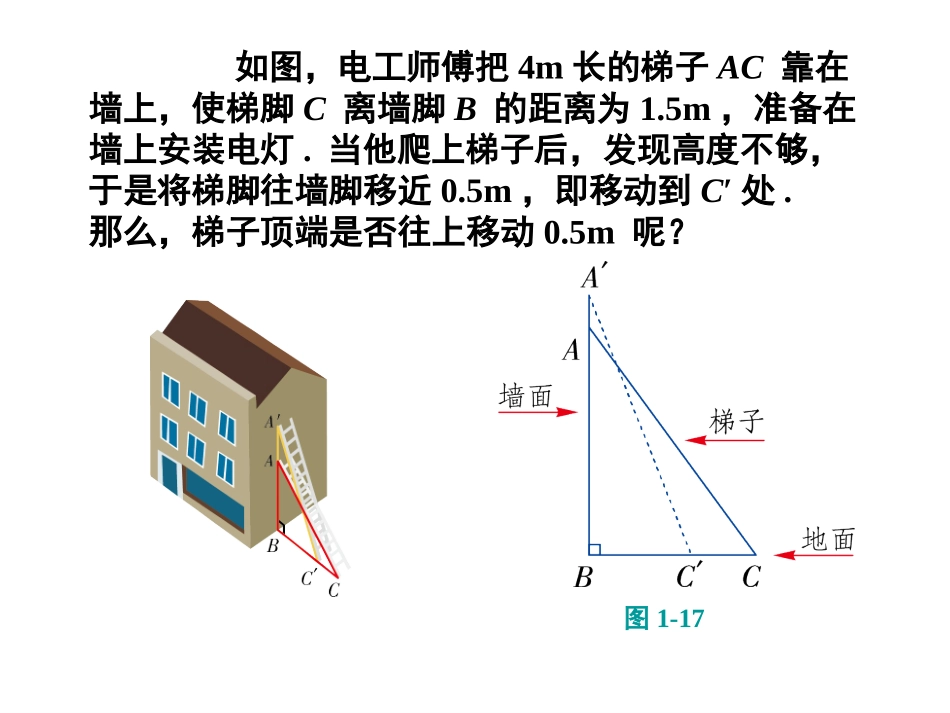
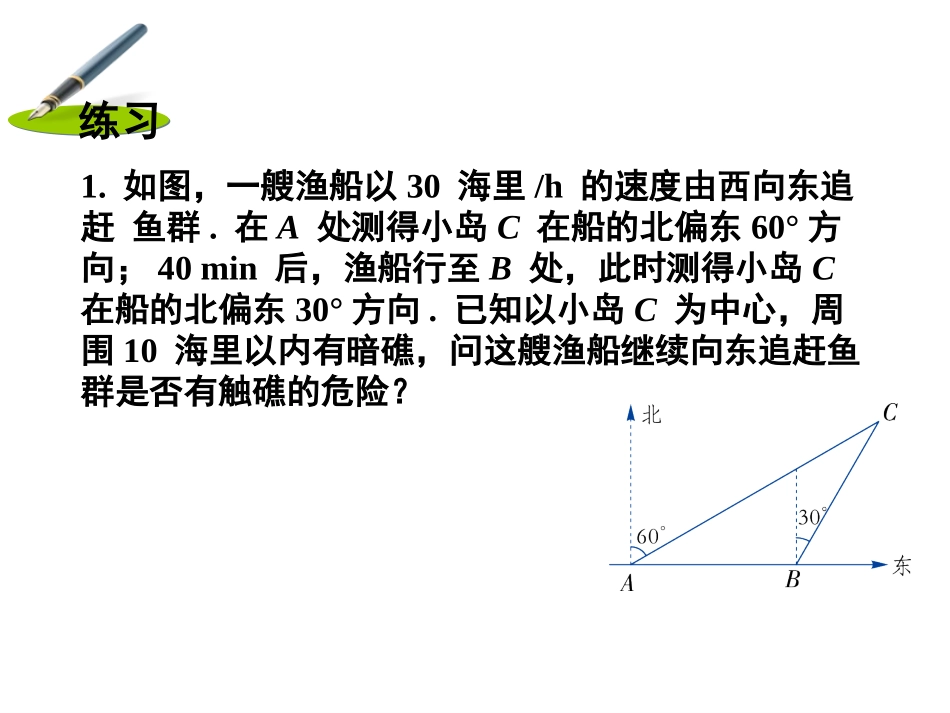
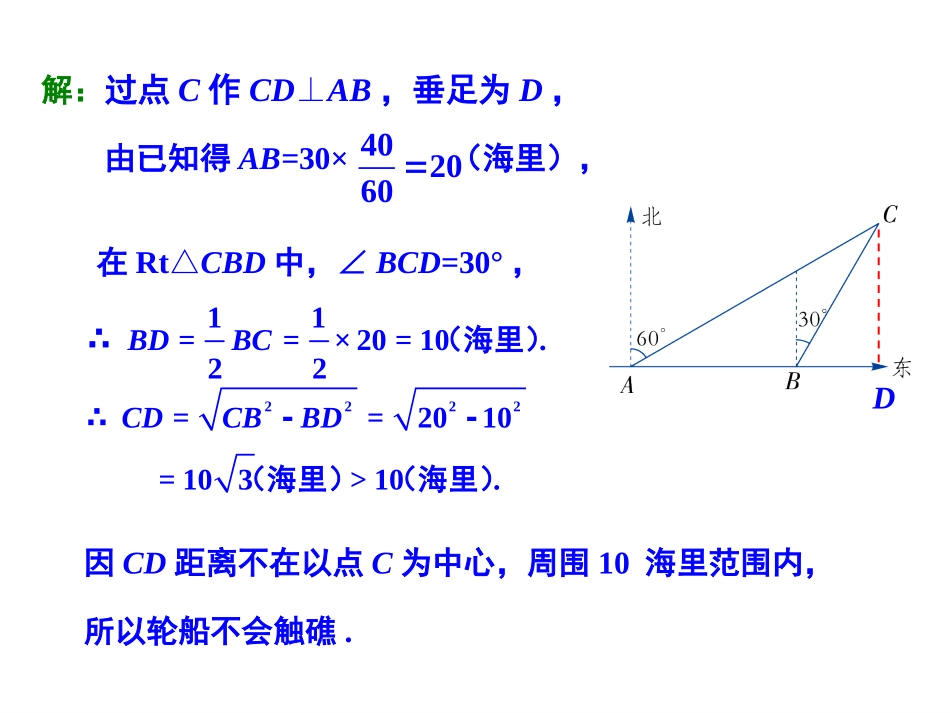
如图,电工师傅把4m长的梯子AC靠在墙上,使梯脚C离墙脚B的距离为1.5m,准备在墙上安装电灯.当他爬上梯子后,发现高度不够,于是将梯脚往墙脚移近0.5m,即移动到C′处.那么,梯子顶端是否往上移动0.5m呢?图1-171.如图,一艘渔船以30海里/h的速度由西向东追赶鱼群.在A处测得小岛C在船的北偏东60°方向;40min后,渔船行至B处,此时测得小岛C在船的北偏东30°方向.已知以小岛C为中心,周围10海里以内有暗礁,问这艘渔船继续向东追赶鱼群是否有触礁的危险?练习解:过点C作CD⊥AB,垂足为D,2222==2010=103>10.CDCBBD∴(海里)(海里)--D因CD距离不在以点C为中心,周围10海里范围内,所以轮船不会触礁.由已知得AB=30×(海里),402060在Rt△CBD中,∠BCD=30°,11×20=10.22∴BD=BC=(海里)(“引葭赴岸”问题)“今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”意思是:有一个边长为10尺的正方形池塘,一棵芦苇生长在池的中央,其出水部分为1尺.如果将芦苇沿与水池边垂直的方向拉向岸边,它的顶端恰好碰到池边的水面.问水深与芦苇长各为多少?例2宋刻《九章算术》书影2.如图,AE是位于公路边的电线杆,高为12m,为了使电线CDE不影响汽车的正常行驶,电力部门在公路的另一边竖立了一根高为6m的水泥撑杆BD,用于撑起电线.已知两根杆子之间的距离为8m,电线CD与水平线AC的夹角为60°.求电线CDE的总长L(A,B,C三点在同一直线上,电线杆、水泥杆的粗细忽略不计).M在下图中,过D点作DM⊥AE,垂足为M.解解M易知四边形MABD为矩形,MA=BD=6m,所以ME=EA-MA=12-6=6(m).在Rt△EMD中,由勾股定理得DEEMDM22226810(m).所以L=ED+CD=10+(m).43M在Rt△DBC中,∠CDB=30°,设BC=x,DC=2x,由勾股定理得,在Rt△DBC中,∠CDB=30°,设BC=x,DC=2x,由勾股定理得,x2+62=(2x)2解得x=.23