锐角三角函数复习2VIP免费

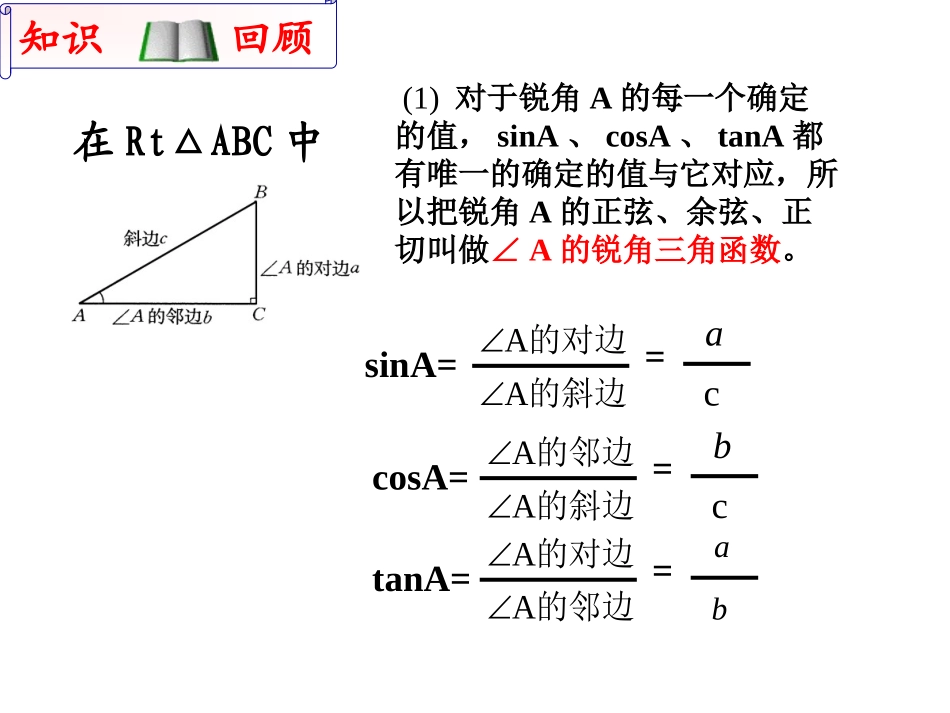
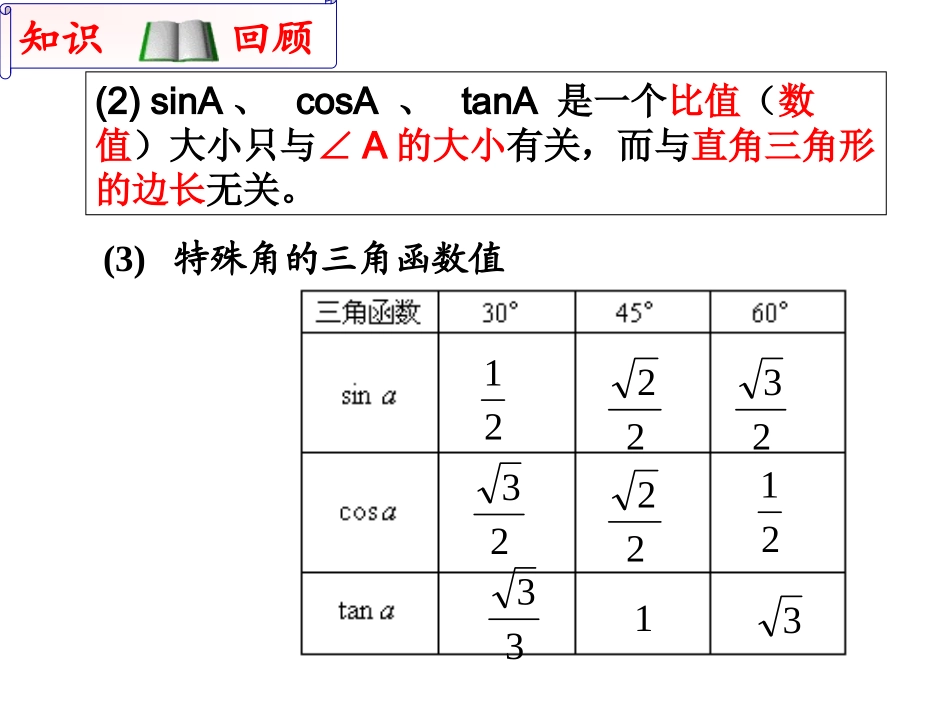
锐角三角函数单元复习锐角三角函数单元复习=ac的斜边的对边AAsinA=在Rt△ABC中=bc的斜边的邻边AAcosA==ab的邻边的对边AAtanA=(1)对于锐角A的每一个确定的值，sinA、cosA、tanA都有唯一的确定的值与它对应，所以把锐角A的正弦、余弦、正切叫做∠A的锐角三角函数。知识回顾知识回顾(2)sinA、cosA、tanA是一个比值（数值）大小只与∠A的大小有关，而与直角三角形的边长无关。(3)特殊角的三角函数值21222323212233131把RtABC△各边长扩大3倍得RtDEF,△那么∠A,D∠的余弦值的关系为（）2在RtABC△中，∠C=900,sinA=,则cosB=()举例224如图,ABC△中,C=90∠0,BD平分∠ABC,BC=12,BD=,则∠A的度数及AD的长为38ADCB举例5如图，已知△ABC中，∠C=300sinA=0.8,AC=10,求AB的长。CAB75°ABC┓D⌒450如图，在△ABC中，已知AC=6，∠C=75°，∠B=45°，求△ABC的面积。⌒⌒60°6练习海中有一个小岛A，它的周围8海里内有暗礁，渔船跟踪鱼群由西向到航行，在B点测得小岛A在北偏东60°方向上，航行12海里到达D点，这时测得小岛A在北偏到30°方向上，如果渔船不改变航线继续向东航行，有没有触礁的危险？BADF解：由点A作BD的垂线交BD的延长线于点F，垂足为F，∠AFD=90°由题意图示可知∠DAF=30°设DF=x,AD=2x则在Rt△ADF中，根据勾股定理222223AFADDFxxx在Rt△ABF中，tanAFABFBF3tan3012xx解得x=666310.4AFx10.4>8没有触礁危险30°60°练习一、基本概念一、基本概念1.正弦ABCacsinA=ca2.余弦bcosA=cb3.正切tanA=ba4.余切cotA=ab锐角锐角AA的正弦、余弦、的正弦、余弦、正切、余切都叫做∠正切、余切都叫做∠AA的锐角三角的锐角三角函数函数..定定义义::练习练习11如右图所示的RtABC⊿中∠C=90°，a=5，b=12，那么sinA=_____，tanA=_____，cosB=______，135125135cotαtanαcosαsinα90°60°45°30°0°角度三角函数二、特殊角三角函数值二、特殊角三角函数值21212222332323333311角度逐渐增大正弦值如何变化?正弦值也增大余弦值如何变化?余弦值逐渐减小正切值如何变化?正切值也随之增大余切值如何变化?余切值逐渐减小思思考考锐角A的正弦值、余弦值有无变化范围？045°时，sinA的值（）(A)小于(B)大于(C)小于(D)大于22222323B(A)小于(B)大于(C)小于(D)大于212123232.当锐角A>30°时，cosA的值（）C☆☆应用练应用练习习1.1.已知角，求值已知角，求值确定角的范围确定角的范围2.2.已知值，求角已知值，求角3.3.确定值的范围确定值的范围(A)小于30°(B)大于30°(C)小于60°(D)大于60°1.当∠A为锐角，且tanA的值大于时，∠A（）33B4.4.确定角的范围确定角的范围232.当∠A为锐角，且cosA的值小于时，∠A（）(A)小于30°(B)大于30°(C)小于60°(D)大于60°B☆☆应用练习应用练习2.2.已知值，求角已知值，求角3.3.确定值的范围确定值的范围3.当∠A为锐角，且cosA=那么（）514.4.确定角的范围确定角的范围(A)0°＜∠A≤30°(B)30°＜∠A≤45°(C)45°＜∠A≤60°(D)6...