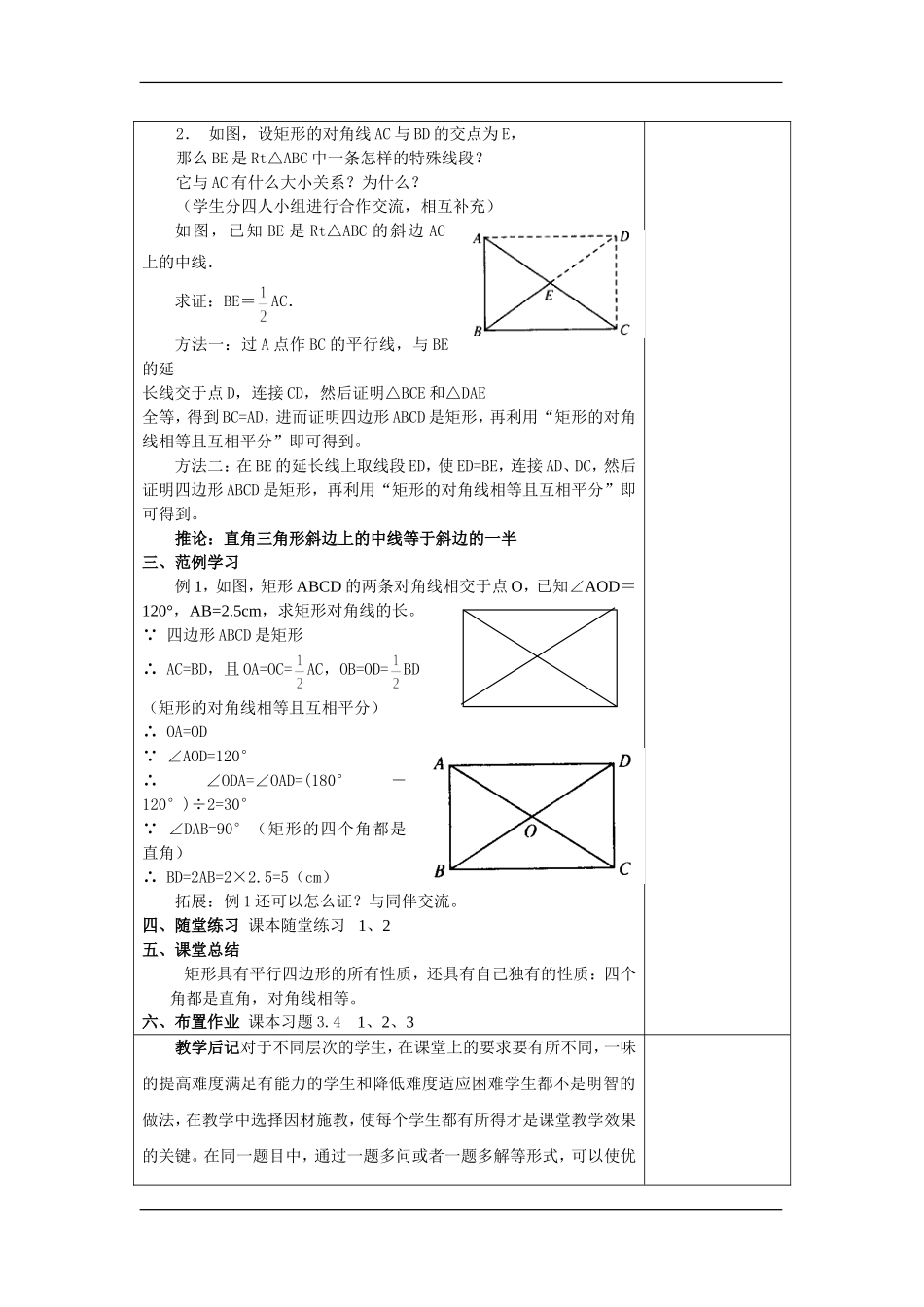
九年级数学教案备课组成员:孙军,石治安,赵晶,岳娜主备人:石治安授课时间:授课班级:授课教师:课题3.2特殊平行四边形(一)课型新授课教学目标1.经历探索、猜想、证明的过程,进一步发展推理论证的能力。2.能运用综合法证明矩形性质定理和判定定理。3.体会证明过程中所运用的归纳概括以及转化等数学思想方法。教学重点掌握矩形的性质和判定以及证明方法。教学难点运用综合法证明矩形性质和判定。教学方法讲练结合法进一步发展推理论证能力,运用综合法证明矩形的性质和判定定理,进一步体会证明的必要性和作用,体会归纳等数学思想方法。教学内容及过程备注一、回顾交流1.你了解哪些特殊的平行四边形?2.这些特殊的平行四边形与平行四边形有哪些关系?3.能用一张图来表示它们之间的关系吗?平行四边形与矩形、菱形、正方形的关系。二、探究新知1.议一议:前面我们已探讨过矩形的性质,矩形的四个角都是直角;矩形的对角线相等.那你能证明它们吗?学生先独立证明两个定理,再进行交流。已知:四边形ABCD是矩形.求证:∠A=∠B=∠C=∠D=90°已知:四边形ABCD是矩形.求证:AC=DB证明:(略)定理矩形的四个角都是直角定理矩形的对角线相等2.如图,设矩形的对角线AC与BD的交点为E,那么BE是Rt△ABC中一条怎样的特殊线段?它与AC有什么大小关系?为什么?(学生分四人小组进行合作交流,相互补充)如图,已知BE是Rt△ABC的斜边AC上的中线.求证:BE=AC.方法一:过A点作BC的平行线,与BE的延长线交于点D,连接CD,然后证明△BCE和△DAE全等,得到BC=AD,进而证明四边形ABCD是矩形,再利用“矩形的对角线相等且互相平分”即可得到。方法二:在BE的延长线上取线段ED,使ED=BE,连接AD、DC,然后证明四边形ABCD是矩形,再利用“矩形的对角线相等且互相平分”即可得到。推论:直角三角形斜边上的中线等于斜边的一半三、范例学习例1,如图,矩形ABCD的两条对角线相交于点O,已知∠AOD=120°,AB=2.5cm,求矩形对角线的长。∵四边形ABCD是矩形∴AC=BD,且OA=OC=AC,OB=OD=BD(矩形的对角线相等且互相平分)∴OA=OD∵∠AOD=120°∴∠ODA=∠OAD=(180°-120°)÷2=30°∵∠DAB=90°(矩形的四个角都是直角)∴BD=2AB=2×2.5=5(cm)拓展:例1还可以怎么证?与同伴交流。四、随堂练习课本随堂练习1、2五、课堂总结矩形具有平行四边形的所有性质,还具有自己独有的性质:四个角都是直角,对角线相等。六、布置作业课本习题3.41、2、3教学后记对于不同层次的学生,在课堂上的要求要有所不同,一味的提高难度满足有能力的学生和降低难度适应困难学生都不是明智的做法,在教学中选择因材施教,使每个学生都有所得才是课堂教学效果的关键。在同一题目中,通过一题多问或者一题多解等形式,可以使优生有所突破,也可以让学困生受到关注,获得解题的成就感,这就对我们的备课和选题提出了更高的要求。