同底数幂的乘法VIP免费

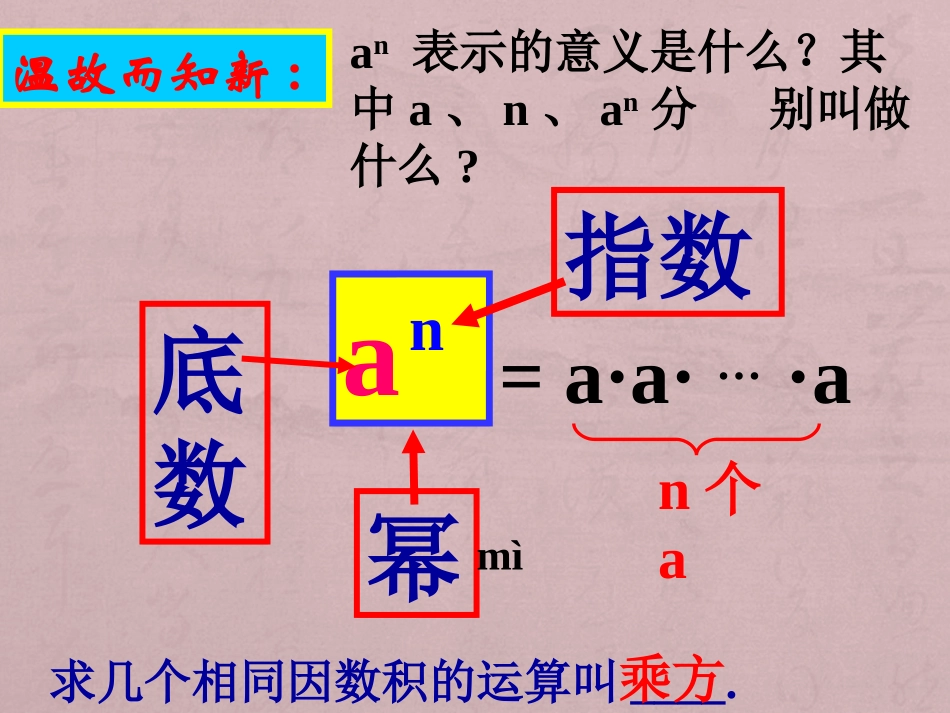
知识与能力知识与能力教学目标教学目标教学目标教学目标1、理解同底数幂的乘法法则2、运用同底数幂的乘法法则进行有关计算．过程与方法过程与方法1、在进一步体会幂的意义时，发展推理能力和有条理的表达能力2、通过“同底数幂的乘法法则”的推导和应用，使学生领会特殊----一般----特殊的认知规律1．体味科学的思想方法，接受数学文化的熏陶，激发探索创新的精神；2．在发展推理能力和有条理的语言、符号表达能力的同时，进一步体会学习数学的兴趣，提高学习数学的信心，感受数学的简洁美；情感态度与价值观情感态度与价值观温故而知新:an指数幂=a·a·…·an个a底数an表示的意义是什么？其中a、n、an分别叫做什么?mì求几个相同因数积的运算叫____.乘方(1)2表示_____________;5(2)10×10×10×10可以写成____;(3)a的底数是__,指数是__;(4)(a+b)的底数是___,指数是__;3(5)(-2)的底数是___,指数是__;4(6)-2的底数是___,指数是__.42×2×2×2×2104a1a+b3-2424回眸·热身合作探究合作探究(1)25×22=()×()=________________=2()；(2)a3×a2=()×()=_______________=a()；(3)5m·5n=()×()=5().2×2×2×2×22×22×2×2×2×2×2×27a×a×aa×aa×a×a×a×a5m+n请同学们根据乘方的意义理解，完成下列填空.思考：观察上面各题左右两边，底数、指数有什么关系？5×···×5m个5n个55×···×525×22=27a3×a2=a55m·5n=5m+n猜想并验证:am.an=(当m、n都是正整数)am·an=m个an个a=aa…a=am+n(m+n)个a即am·an=am+n(当m、n都是正整数)（aa…a）（aa…a）（乘方的意义）（乘法结合律）（乘方的意义）am+n1.我是法官我来判（1）b5·b5=2b5（）（2）b5+b5=b10（）（3）x5·x5=x25()（4）y5·y5=2y10()（5）c·c3=c3()（6）m+m3=m4()m+m3=m+m3b5·b5=b10b5+b5=2b5x5·x5=x10y5·y5=y10c·c3=c4××××××2、计算：（1）-a2·a6；解：（2）(-x)·(-x)3原式=(-x)1+3=(-x)4=-a8=x4原式=-a2+6解：（3）（-3）2×（-3）7解：原式=(-3)2+7=(-3)9=-39（4）xm-2·x2m+1解：原式=x（2m-2）+（2m+1）=x4m-1(5)(x+y)3·(x+y)4·(y-x)3(6)(x-y)2(7)(x-y)3·(y-x)1.1.填空：填空：（（11））xx55··（）（）=x=x88（（22））a·a·（（））==aa66（（33））x·xx·x33()=x()=x77（（44））xxmm··（）（）＝ｘ＝ｘ3m3m举一反三举一反三,,拓展提升拓展提升xx33aa55xx33ｘｘ2m2m2.2.已知已知:a:a55=7;a=7;a33=16.=16.求求aa88的值的值本节课你感悟到了什么？同底数幂相乘，底数指数am·an=am+n(m、n正整数)整理反思我学到了什么？知识方法“特殊→一般→特殊”例子公式应用不变，相加.数学沙龙数学沙龙,,智慧无限智慧无限..(1)(1)已知已知:8×4=2:8×4=2xx,,则则x=(x=())(2)(2)计算：（计算：（-2-2））20062006-2-220072007