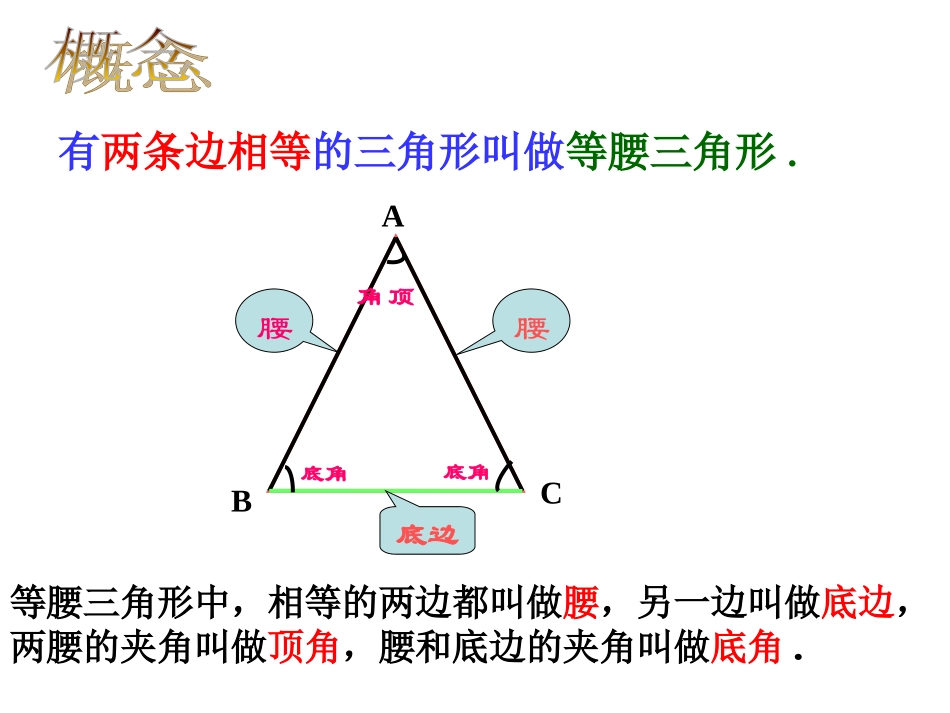
13.3.1等腰三角形(一)1、等腰三角形一腰为3cm,底为4cm,则它的周长是;2、等腰三角形的一边长为3cm,另一边长为4cm,则它的周长是;3、等腰三角形的一边长为3cm,另一边长为8cm,则它的周长是。10cm10cm或11cm19cm复习有两条边相等的三角形叫做等腰三角形.等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.ACB腰腰底边顶角底角底角如图所示,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC有什么特点?ABCD探究想一想1、上面剪出的等腰三角形是轴对称图形吗?2、把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角。3、由这些重合的线段和角,你能发现等腰三角形的哪些性质呢?说一说你的猜想。重合的线段重合的角ACBDAB=ACBD=CDAD=AD∠B=∠C.∠BAD=∠CAD∠ADB=∠ADC等腰三角形除了两腰相等以等腰三角形除了两腰相等以外外,,你还能发现它的其他性质吗你还能发现它的其他性质吗??大胆猜想猜想与论证等腰三角形的两个底角相等。已知:△ABC中,AB=AC求证:∠B=C分析:1.如何证明两个角相等?2.如何构造两个全等的三角形?猜想ABCDABC则有∠1=∠2D12在△ABD和△ACD中证明:作顶角的平分线AD,AB=AC∠1=∠2AD=AD(公共边)∴△ABD≌△ACD(SAS)∴∠B=∠C(全等三角形对应角相等)ABC则有BD=CDD在△ABD和△ACD中证明:作△ABC的中线ADAB=ACBD=CDAD=AD(公共边)∴△ABD≌△ACD(SSS)∴∠B=∠C(全等三角形对应角相等)ABC则有∠ADB=∠ADC=90ºD在RtABD△和RtACD△中证明:作△ABC的高线ADAB=ACAD=AD(公共边)∴Rt△ABD≌Rt△ACD(HL)∴∠B=∠C(全等三角形对应角相等)猜想与论证等腰三角形的两个底角相等。性质1(等边对等角)ABCD猜想∵AB=AC(已知)∴∠B=C∠(等边对等角)∵AB=AC(已知)∴∠B=C∠(等边对等角)几何语言:⒈等腰三角形一个底角为75°,它的另外两个角为_______;⒉等腰三角形一个角为70°,它的另外两个角为___________________;⒊等腰三角形一个角为110°,它的另外两个角为________。75°,30°70°,40°或55°,55°35°,35°小试牛刀想一想想一想::刚才的证明除了能得到∠B=∠C你还能发现什么?重合的线段重合的角ABDCAB=ACBD=CDAD=AD∠B=∠C.∠BAD=∠CAD∠ADB=∠ADC=90°等腰三角形的等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合。性质2(等腰三角形三线合一)ABCD∵AB=AC,BD=CD(已知)∴∠BAD=CAD∠,ADBC⊥(三线合一)∵AB=AC,BD=CD(已知)∴∠BAD=CAD∠,ADBC⊥(三线合一)∵AB=AC,∠BAD=CAD∠(已知)∴BD=CD,ADBC⊥(三线合一)∵AB=AC,∠BAD=CAD∠(已知)∴BD=CD,ADBC⊥(三线合一)∵AB=AC,ADBC⊥(已知)∴BD=CD,∠BAD=CAD∠(三线合一)∵AB=AC,ADBC⊥(已知)∴BD=CD,∠BAD=CAD∠(三线合一)几何语言:已知:如图,△ABC中,AB=AC,AD是底边BC的中线.求证:∠BAD=∠CAD,AD⊥BC.ABCD证明:∵AD是底边BC的中线,∴BD=CD.∵AB=AC,BD=CD,AD=AD,∴△ABD≌△ACD(SSS).∴∠BAD=∠CAD,∠ADB=∠ADC.∵∠ADB+∠ADC=180°,∴∠ADB=90°.∴AD⊥BC.例1、如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。ABCD解:∵AB=AC,BD=BC=AD,∴∠ABC=C=BDC∠∠,∠A=ABD∠(等边对等角)设∠A=x°,则∠BDC=A+ABD=2x∠∠°,从而∠ABC=C=BDC=2x∠∠°,于是在△ABC中,有∠A+ABC+C=x+2x∠∠+2x=180,解得x=36,在△ABC中,∠A=36°,∠ABC=C=72°∠x⌒2x⌒2x⌒⌒2x答:∠A=36°ABC=C=72°∠∠轴对称图形两个底角相等,简称“等边对等角”顶角平分线、底边上的中线、和底边上的高互相重合,简称“三线合一”