曲线与方程习题课展VIP免费

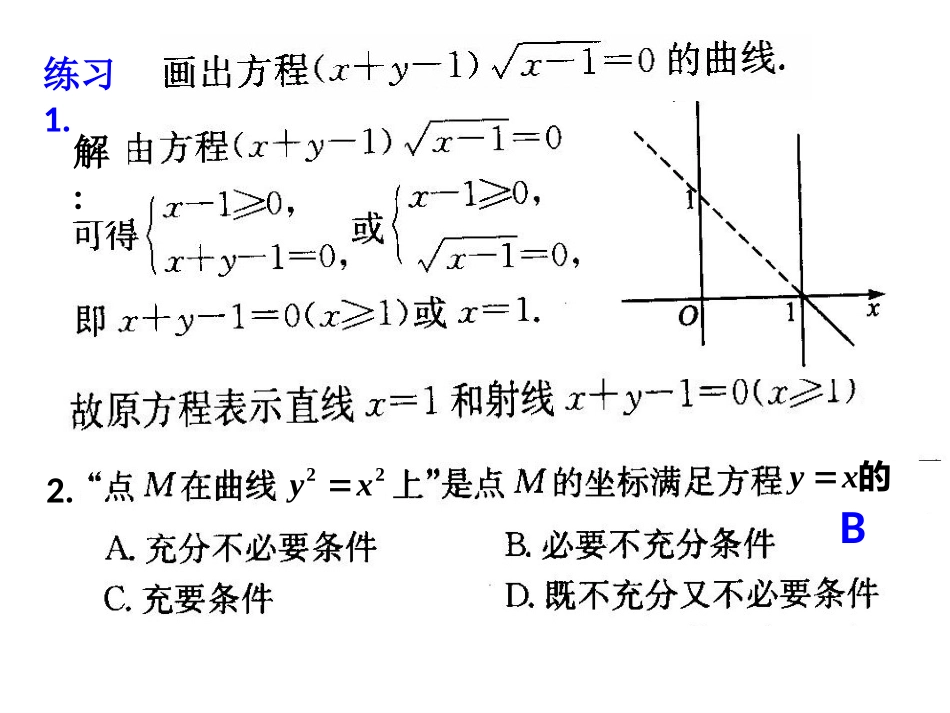
曲线方程习题课求曲线的方程(轨迹方程)的一般步骤:一、建立适当的坐标系，设曲线上任一点的坐标，及相关点的坐标;二、(限)找条件，由条件(代)列方程;三、化简方程.证明所得方程(可以省略)为所求的曲线方程.以上步骤用一句话概括就是:建设现．．．(．限．)．代化．．.复习：解:练习1.22yxyx的2.BB3.4.到F(2，0)和y轴的距离相等的动点的轨迹方程是____解:设动点为(x，y)，则由题设得化简得:y2=4(x-1)这就是所求的轨迹方程.y2=4(x-1)5.在三角形ABC中，若|BC|=4，BC边上的中线AD的长为3，求点A的轨迹方程.设A(x，y)，又D(0，0)，所以3yx|AD|22化简得:x2+y2=9(y≠0)这就是所求的轨迹方程.解:取B、C所在直线为x轴，线段BC的中垂线为y轴，建立直角坐标系.,(5,0),(5,0),,(0),ABCABACBCmmC练习1、已知的两个顶点的坐标分别是且所在直线的斜率之积等于试探求顶点的轨迹方程。解：设C（x，y）．由已知，得直线AC的斜率kAC＝5yx（x≠－5）；直线BC的斜率kBC＝5yx（x≠5）；由题意，得kACkBC＝m，所以，5yx×5yx＝m（x≠±5）．写成225x－225ym＝1（x≠±5）．（直接法）1.直接法:求轨迹方程最基本的方法,直接通过建立x,y之间的关系,构成F(x,y)=0即可.①直接法②定义法③代入法④参数法求轨迹方程的常见方法:3.代入法:这个方法又叫相关点法或坐标代换法.即利用动点P’(x’,y’)是定曲线F(x,y)=0上的动点,另一动点P(x，y)依赖于P’(x’,y’)，那么可寻求关系式x’=f(x,y),y’=g(x,y)后代入方程F(x’,y’)=0中，得到动点P的轨迹方程.2.定义法：如果能够确定动点的轨迹满足某种已知曲线的定义，则可用曲线定义写出方程。例3.已知△ABC,A(-2,0),B(0,-2),第三个顶点C在曲线y=3x2-1上移动,求△ABC的重心的轨迹方程.相关点法4.参数法:选取适当的参数,分别用参数表示动点坐标x,y,得出轨迹的参数方程，消去参数，即得其普通方程。例:已知点C的坐标是（2，2），过点C的直线CA与x轴交于点A，过点C且与直线CA垂直的直线与y轴交于点B，设点M是线段AB的中点，求点M的轨迹方程。yx0CABM10例1.△ABC的顶点B、C的坐标分别为(0,0)、(4,0),AB边上的中线的长为3,求顶点A的轨迹方程.xy0(,)xy解:设A的坐标分别为(,)xy,AB的中点D的坐标为11(,)xy由中点坐标公式可知1122xxyy∴2211(4)9xy化简整理得22(8)36xy∴点A的轨迹方程为22(8)36xy.0yCABD AB边上的中线CD=3M法二:添辅助线MA,巧用图形性质,妙极了!注:这种求轨迹方程的方法叫做相关点坐标分析法(代入法)思考211xy0ABCMlO解:设M(,)xy设226490xyxy的圆心为C,则C的坐标为(3,2).且13OC M为AB的中点,∴由圆的性质可知MC⊥OM∴点M在以OC为直径的圆O上.∴OC的中点O的坐标为3(,1)2 圆O的方程为22313()(1)24xy(下面同法一)返回妙!例2.经过原点的直线l与圆226490xyxy相交于两个不同点A、B，求线段AB的中点M的轨迹方程.12xy0ABCMl解:设M(,)xy,A11(,)xy,B22(,)xy则121222xxxyyy设直线l的方程为ykx由方程组2264100ykxxyxy消去y得22(1)(64)90kxkx121222649,11kxxxxkk∴22321321kxkkykk消去参数k得22320xyxy返回例2.经过原点的直线l与圆226490xyxy相交于两个不同点A、B，求线段AB的中点M的轨迹方程.求曲线的方程(轨迹方程)的一般步骤:一、建立适当的坐标系，设曲线上任一点的坐标，及相关点的坐标;二、(限)找条件，由条件(代)列方程;三、化简方程.证明所得方程(可以省略)为所求的曲线方程.以上步骤用一句话概括就是:建设现．．．(．限．)．代化．．.2225xy22(3)48xy16作业(选做题):1.动点在圆122yx上移动时，它与定点)0,3(B连线的中点的轨迹方程是()(A)4)3(22yx(B)1)3(22yx(C)14)32(22yx(D)21)23(22yx2.点M(,)xy与定点F(1,0)距离和它到直线8x的距离的比为12,则动点M的轨迹方程为()(A)22143xy(B)22187xy(C)2211612xy(D)2234860xyx=0CD练习1.已知点M与x轴的距离和点M...