程序框图与条件结构VIP免费

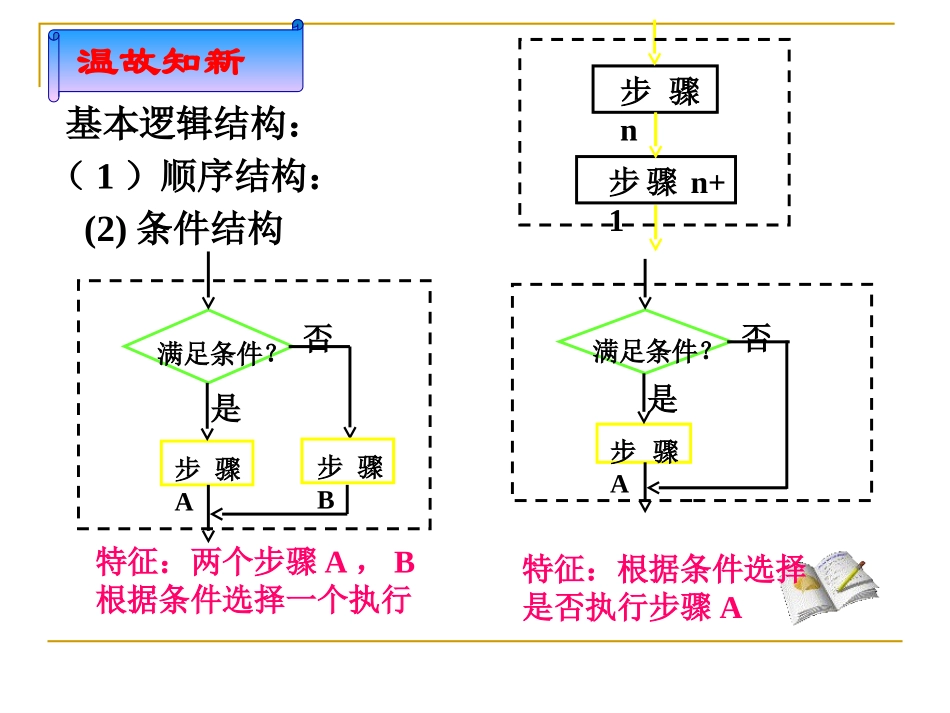
温故知新步骤n步骤n+1基本逻辑结构：(2)条件结构（1）顺序结构：满足条件？步骤A步骤B是否满足条件？步骤A是否特征：两个步骤A，B根据条件选择一个执行特征：根据条件选择是否执行步骤A循环结构1.需要重复执行同一操作的结构称为循环结构。即从某处开始，按照一定条件反复执行某一处理步骤。反复执行的处理步骤称为循环体。循环结构有两种形式：当型循环结构和直到型循环结构。①直到型循环结构：循环体满足条件？是否特征：在执行了一次循环体后，对条件进行判断，如果条件不满足，就继续执行循环体，直到条件满足时终止循环.循环体满足条件？是否②当型循环结构：特征：在每次执行循环体前，对条件进行判断，如果条件满足，就执行循环体，否则终止循环.从以上不同形式的循环结构可看出，循环结构中一定包含条件结构，用于何时终止执行循环体。设计一算法,求和:1+2+3+…+100.第一步:确定首数a,尾数b,项数n；第二步:利用公式“总和=(首数+尾数)×项数/2”求和；第三步:输出求和结果.算法1：开始结束输入a,b,nS=(a+b)*n/2输出S新课引入算法2：第一步:从1开始将自然数1,2,3,…,100逐个相加;第二步:输出累加结果.1.上边的式子有怎样的规律呢？2.怎么用程序框图表示呢？S=S+i设计一算法,求和:1+2+3+…+100.S=0S=S+1S=S+2S=S+3…S=S+100思考：在一些算法中,经常会出现从某处开始,反复执行某一处理步骤,这就是循环结构.例1.设计一个计算1+2+3+…+100的程序框图.开始i≤100?否是输出s结束i=1S=0i=i+1S=S+i解：由于加数较多，采用逐个相加的方法程序太长，是不可取的，因此应采取引入变量应用循环的办法。开始i=1i>100？是输出S结束S=0i=i+1S=S+i否（2）程序框图：例1.设计一个计算1+2+3+…+100的程序框图.第四步，若i>100成立，则输出S，结束算法；否则，返回第二步.第一步，令i=1，S=0.第二步，S=S+i.第三步，i=i+1.解：算法步骤：注：在写循环结构的算法时，最关键是确定循环结构。（1）确定循环体：S=S+i，i=i+1（2）确定初始变化量：i=1，S=0.（3）设定循环控制条件：①直到型：i>100;(满足条件结束）；②当型：i≤100;(不满足条件结束）；例1.设计一个计算1+2+3+…+100的程序框图.开始1isum1iiiss100i？s输出结束是否程序框图：s输出结束开始1i0sisssum1ii？100i是否当型循环结构直到型循环结构0s练习2：1.如图（1）为循环体中的循环，它换成另外一种循环的框图Ｐ＞Ｑ？a图(1)是否aＰ<=Ｑ？是否2.如图(2)的算法功能是结束开始2i2ii2,ii输出(图2)是否?624)2(ii当型求积为624的相邻偶数.直到型3.指出程序框图的运算结果？开始1iisumsumsum1ii?sum输出0sum结束是否5i输出sum.154.下图为求1~1000的所有的偶数的和而设计的一个程序框图,将空白处补上,并指明它是循环结构中的哪一种类型,并画出它的另一种循环结构框图．开始i=2sum=0i<=1000输出sum结束sum=sum+ii=i+2设计一算法，求积:1×2×3×…×100，画出流程图结束输出Ai=0，A=1开始i=i+1A=A*ii>=100?否是课堂练习某工厂2005年的年生产总值为200万，技术革新以后每年的年生产总值比上一年增长5％。设计一个程序框图，输出预计年生产总值超过300万元的最早年份。解：（1）算法步骤：第一步，输入2005年的年生产总值。第二步，计算下一年的年生产总值。第三步，判断所得的结果是否大于300.若是，则输出该年的年份；否则，返回第二步例题剖析2由于“第二步”是重复操作的步骤，所以可以用循环结构来实现。我们按照“确定循环体”、“初始化变量”、“设定循环控制条件”的顺序来构造循环结构。（2）初始化变量：若将2005年的年生产总值堪称计算的起始点，则n的初始值为2005，a的初始值为200.（3）设定循环控制条件：当“年生产总值超过300万元”时终止循环，所以可通过判断“a>300”是否成立来控制循环。（1）确定循环体：设a为某年的年生产总值，t为年生产总值的年增长量，n为年份，则循环体为0.051taaatnn程序框图:开始n=2005a=200t=0.05an=n+1a>300?是输出n结束否a=a+t课堂小结本节课主要学习了循环结构，特别注意理解以下几个问题：1.两种循环结构框图及其特征。...