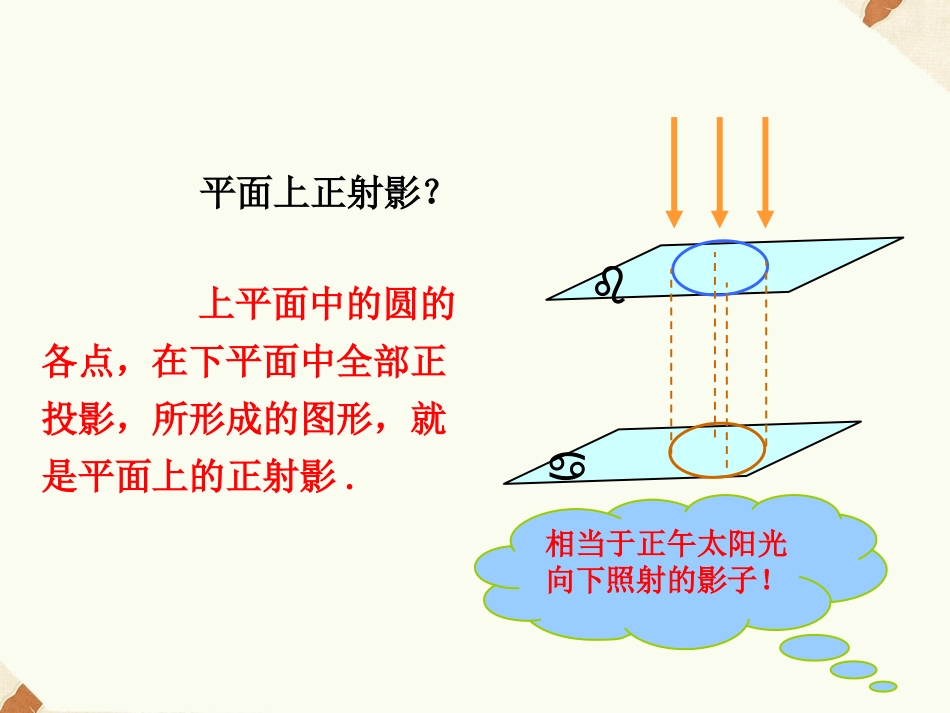
直线上正射影?相当于太阳光向下照射的影子!lBAABAA⊥lBB⊥lAABBABAB旧知回顾旧知回顾旧知回顾旧知回顾平面上正射影?相当于正午太阳光向下照射的影子!上平面中的圆的各点,在下平面中全部正投影,所形成的图形,就是平面上的正射影.平行射影?上平面中的圆的各点,沿着一组平行线l作为投影方向,在下平面投影所形成的图形,就是平行射影.如图,AB、CD是两个等圆的直径,AB//CD,AD、BC与两圆相切.作两圆的公切线EF,切点分别为F1,F2,交BA、DC的延长线于E、F,交AD于G1,交BC于G2,设EF与BC、CD的交角分别为、探究由切线长定理有G2F1=G2B,G2F2=G2C,∴G2F1+G2F2=G2B+G2C=BC=AD又∵G1G2=G1F2+F2G2由切线长定理知G1F2=G1D,F2G2=G2C,∴G1G2=G1D+G2C连接F1O1,F2O2,容易证明△EF1O1≌△FF2O2∴EO1=FO2解析又∵O1A=O2C,∴EA=FC于是可证得△FCG2≌△EAG1∴G1A=G2C∴G1G2=G1D+G1A=AD在Rt△G2EB中22122cosGBGFGEGE∴G2F1=G2Ecos又∵=90-∴G2F1=G2Ecos=G2Esin由此得到结论:(1)G2F1+G2F2=AD(2)G1G2=AD212(3)cossinGFGE将左图中的两个圆拓广为球面,将矩形ABCD看成是圆柱面的轴截面,将EB、DF拓广为两个平面、,EF拓广为平面,得到右图.探究你能猜想这个椭圆的两个焦点的位置吗?猜想:两个焦点为两个球与斜截面的切点上,即过球心O1、O2分别作斜截面的垂线,其垂足F1、F2就可以能是焦点.猜想猜想对截口上任一点P,证明:PF1+PF2=定值当点P与G2重合时,有G2F1+G2F2=AD当点P不在端点时,连接PF1,PF2,则PF1,PF2分别是两个球面的切线,切点为F1,F2.过P作母线,与两球面分别相交于K1,K2,则PK1,PK2分别是两球面的切线,切点为K1,K2PF1=PK1,PF2=PK2,PF1+PF2=PK1+PK2=AD知识要知识要点点知识要知识要点点圆柱形物体的斜截口是椭圆.课堂小结课堂小结课堂小结课堂小结圆柱形物体的斜截口是椭圆.1.如下图,指出圆柱被平面所截得图形是什么?课堂练习课堂练习课堂练习课堂练习解析截面是一个椭圆谢谢观看!