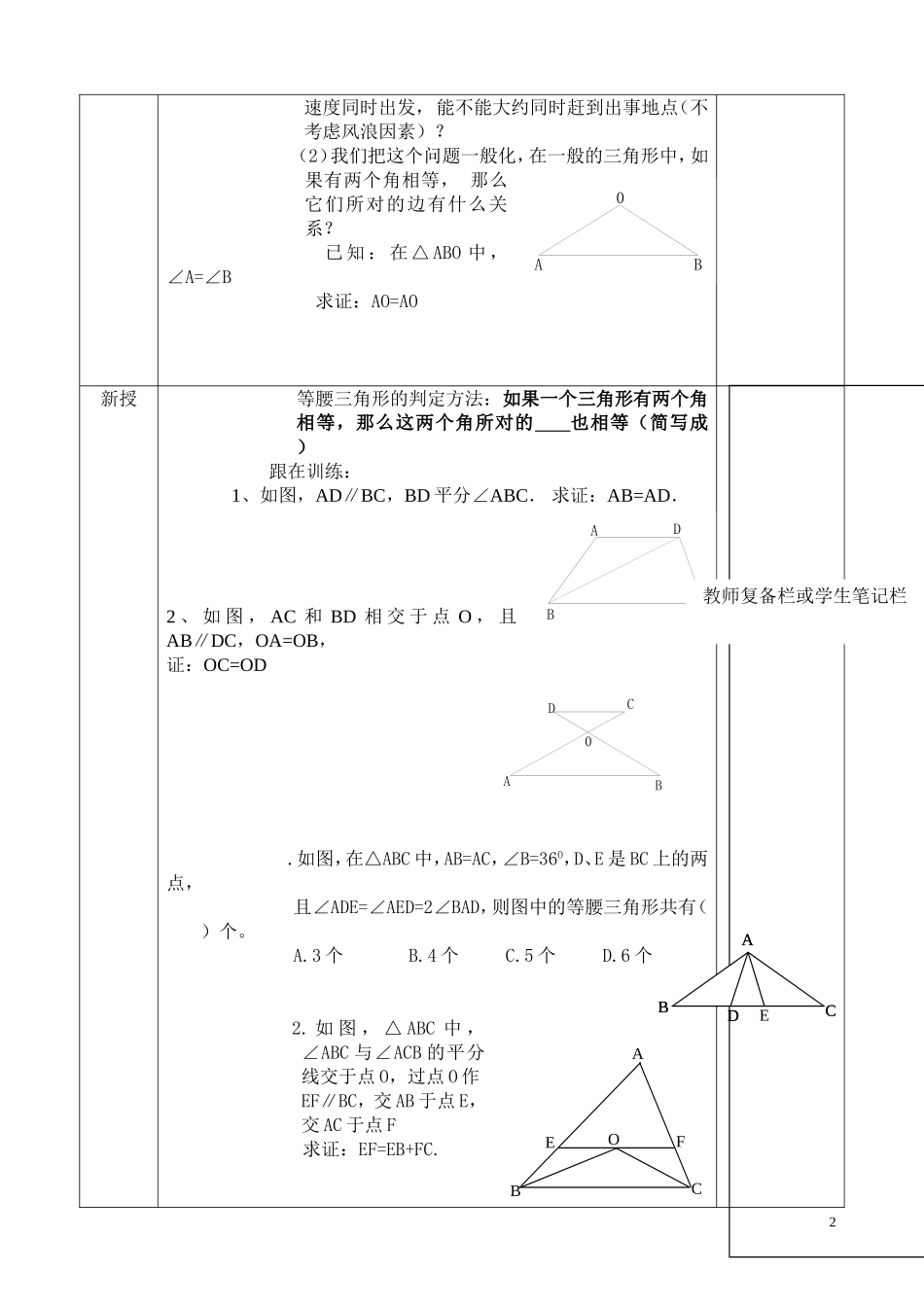
学科教师姓名授课班级教学内容13.3.1等腰三角形(2)计划课时1教材分析理解等腰三角形的判定方法及应用。学情分析通过对等腰三角形的判定方法的探索,体会探索学习的乐趣教学策略选择与设计教学资源与工具设计通过对等腰三角形的判定方法的探索,体会探索学习的乐趣教学目标知识与技能过程与方法理解等腰三角形的判定方法及应用。情感态度与价值观教学重点等腰三角形的判定方法及其应用教学难点等腰三角形的判定方法及其应用教学准备教学过程设计意图预习检查1.等腰三角形的概念?2.等腰三角形有几条判定定理,分别是什么?导入新课1、等腰三角形的两边长分别为6,8,则周长为2、等腰三角形的周长为14,其中一边长为6,则另两边分别为3、等腰三角形的一个角为70°,则另外两个角的度数是4、等腰三角形的一个角为120°则另外两个角的度数是5、如图,在△ABC中,AB=AC,(1)若AD平分∠BAC,那么、(2)若BD=CD,那么、(3)若AD⊥BC,那么、探究点一:等腰三角形的判定1、1、思考:(1)如图,位于在海上A、B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B.如果这两艘救生船以同样的1速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?(2)我们把这个问题一般化,在一般的三角形中,如果有两个角相等,那么它们所对的边有什么关系?已知:在△ABO中,∠A=∠B求证:AO=AO新授等腰三角形的判定方法:如果一个三角形有两个角相等,那么这两个角所对的也相等(简写成)跟在训练:1、如图,AD∥BC,BD平分∠ABC.求证:AB=AD.2、如图,AC和BD相交于点O,且AB∥DC,OA=OB,证:OC=OD.如图,在△ABC中,AB=AC,∠B=36O,D、E是BC上的两点,且∠ADE=∠AED=2∠BAD,则图中的等腰三角形共有()个。A.3个B.4个C.5个D.6个2.如图,△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作EF∥BC,交AB于点E,交AC于点F求证:EF=EB+FC.2AB0DCAB教师复备栏或学生笔记栏DCAB0DCBAEDCBAACBFEO3、如图,∠A=∠B,CE∥DA,CE交AB于E,求证△CEB是等腰三角形小结等腰三角形的判定方法:如果一个三角形有两个角相等,那么这两个角所对的也相等(简写成)作业布置板书设计等腰三角形的判定方法:如果一个三角形有两个角相等,那么这两个角所对的也相等(简写成)3课堂评价反馈设计教学反思4