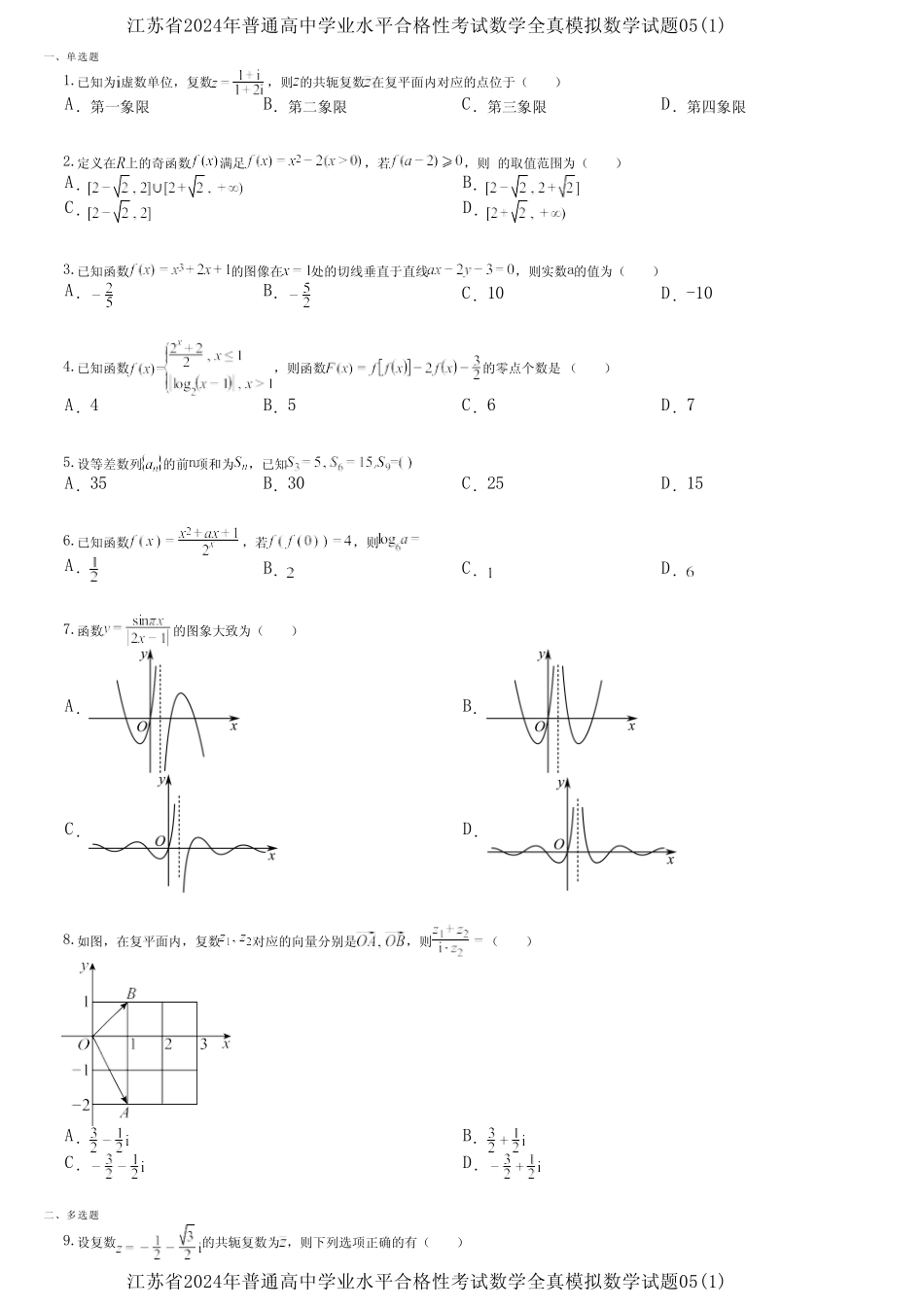
一、单选题二、多选题1.已知为虚数单位,复数,则的共轭复数在复平面内对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限2.定义在上的奇函数满足,若,则的取值范围为()A.B.C.D.3.已知函数的图像在处的切线垂直于直线,则实数a的值为()A.B.C.10D.-104.已知函数,则函数的零点个数是()A.4B.5C.6D.75.设等差数列的前n项和为,已知A.35B.30C.25D.156.已知函数,若,则A.B.C.D.7.函数的图象大致为()A.B.C.D.8.如图,在复平面内,复数对应的向量分别是,则()A.B.C.D.9.设复数的共轭复数为,则下列选项正确的有()江苏省2024年普通高中学业水平合格性考试数学全真模拟数学试题05(1)江苏省2024年普通高中学业水平合格性考试数学全真模拟数学试题05(1)三、填空题四、解答题A.B.C.D.10.19世纪时期,数学家们处理大部分数学对象都没有完全严格定义,数学家们习惯借助直觉和想象来描述数学对象,德国数学家狄利克雷(Dirichlet)在1829年给出了著名函数:(其中为有理数集,为无理数集),后来人们称之为狄利克雷函数,狄利克雷函数的出现表示数学家们对数学的理解发生了深刻的变化,数学的一些“人造”特征开始展现出来,这种思想也标志着数学从研究“算”转变到了研究“概念、性质、结构”.一般地,广义狄利克雷函数可以定义为(其中且),则下列说法正确的是()A.都有B.函数和均不存在最小正周期C.函数和均为偶函数D.存在三点在图像上,使得为正三角形,且这样的三角形有无数个11.下列命题中正确的是()A.若样本数据,,…,的平均数是11,方差为8,则数据,,…,的平均数是6,方差为2B.已知随机变量服从正态分布,且,则C.已知两个变量具有线性相关关系,其回归方程为,且数据样本中心点为,则当时,样本的估计值为7D.随机变量,若,,则12.设定义在R上的函数满足:①:②对任意实数满足;③存在大于零的常数m,使得,且当时,.则()A.B.当时,C.函数在R上没有最值D.任取13.已知变量,的关系可以用模型拟合,设,其变换后得到一组数据如下:468102356由上表可得线性回归方程,则______.14.已知椭圆:()的左,右焦点分别为,,点,在椭圆上,且满足,,则椭圆的离心率为________.15.如图,小方格是边长为1的正方形,图中粗线画出的是某几何体的三视图,正视图中的曲线为四分之一圆弧,则该几何体的表面积是___________.16.在中,角的对边分别为,已知(1)求的值;(2)若,求的面积.17.在中,角A,B,C的对边分别为a,b,c,若.(1)求证:;(2)若,点D为边AB上的一点,CD平分,,求边长.18.长江十年禁渔计划全面施行,渔民老张积极配合政府工作,如期收到政府的补偿款.他决定拿出其中10万元进行投资,并看中了两种为期60天(视作2个月)的稳健型(不会亏损)理财方案.方案一:年化率,且有的可能只收回本金;方案二:年化率,且有的可能只收回本金;已知老张对每期的投资本金固定(都为10万元),且第一次投资时选择了方案一,在每期结束后,老张不间断地进行下一期投资,并且他有的可能选择另一种理财方案进行投资.(1)设第i次投资()选择方案一的概率为,求;(2)求一年后老张可获得总利润的期望(精确到1元).注:若拿1千元进行5个月年化率为的投资,则该次投资获利元.19.已知是椭圆C:上的动点,过原点O向圆M:引两条切线,分别与椭圆C交于P,Q两点(如图所示),记直线OP,OQ的斜率依次为,,且.(1)求圆M的半径r;(2)求证:为定值;(3)求四边形OPMQ的面积的最大值.20.某数学建模小组研究挡雨棚(图1),将它抽象为柱体(图2),底面与全等且所在平面平行,与各边表示挡雨棚支架,支架、、垂直于平面.雨滴下落方向与外墙(所在平面)所成角为(即),挡雨棚有效遮挡的区域为矩形(、分别在、延长线上).(1)挡雨板(曲面)的面积可以视为曲线段与线段长的乘积.已知米,米,米,小组成员对曲线段有两种假设,分别为:①其为直线段且;②其为以为圆心的圆弧.请分别计算这两种假设下挡雨板的面积(精确到0.1平方米);(2)小组拟自制部分的支架用于测试(图3),其中米,,,其中,求有效遮挡区域高的最大值.21.已知的内角,,的对边分别为,,,向量(1)当时,求的值;(2)当时,且,求的值.