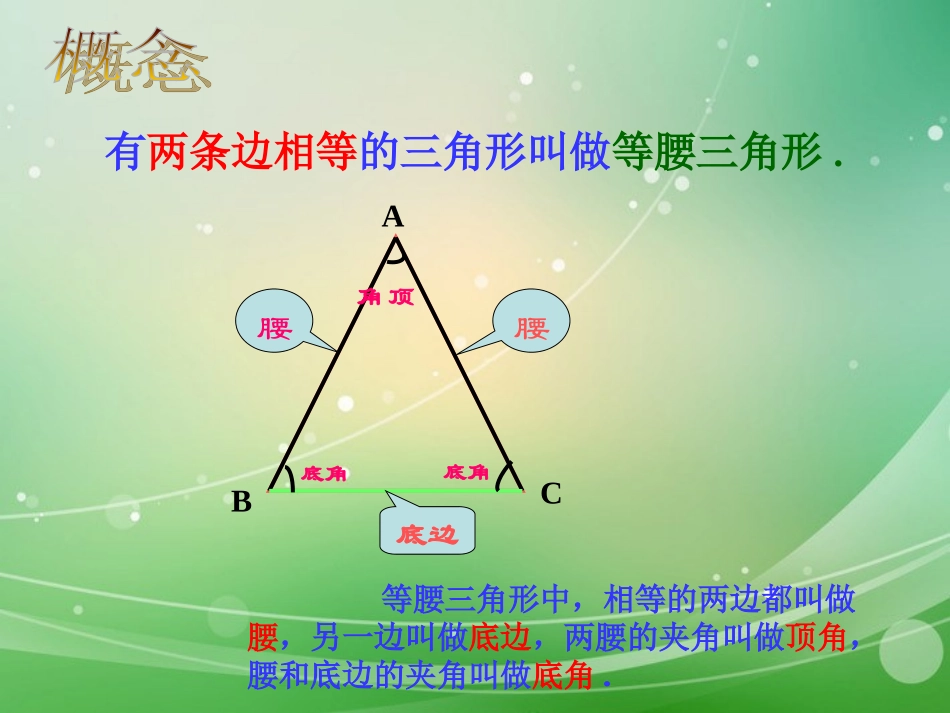
动手做一做ACB△ABC有什么特点?看一看有两条边相等的三角形叫做等腰三角形.等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.ACB腰腰底边顶角底角底角1、等腰三角形一腰为3cm,底为4cm,则它的周长是;2、等腰三角形的一边长为3cm,另一边长为4cm,则它的周长是;3、等腰三角形的一边长为3cm,另一边长为8cm,则它的周长是。10cm10cm或11cm19cm我能行把剪出的等腰三角形ABC沿折痕对折,找出其中相等的线段和角.等腰三角形是轴对称图形吗?※等腰三角形是轴对称图形,对称轴是对称轴是顶角平分线所在的直线顶角平分线所在的直线。相等的线段相等的角ACBDAB=ACBD=CDAD=AD∠B=∠C∠BAD=∠CAD∠ADB=∠ADC等腰三角形除了两腰相等以等腰三角形除了两腰相等以外外,,你还能发现它的其他性质吗你还能发现它的其他性质吗??大胆猜想猜想与论证等腰三角形的两个底角相等。已知:△ABC中,AB=AC求证:∠B=C分析:1.如何证明两个角相等?2.如何构造两个全等的三角形?猜想ABCDABC则有∠1=∠2D12在△ABD和△ACD中证明:作顶角的平分线AD,AB=AC∠1=∠2AD=AD(公共边)∴△ABD≌△ACD(SAS)∴∠B=∠C(全等三角形对应角相等)ABC则有BD=CDD在△ABD和△ACD中证明:作△ABC的中线ADAB=ACBD=CDAD=AD(公共边)∴△ABD≌△ACD(SSS)∴∠B=∠C(全等三角形对应角相等)ABC则有∠ADB=∠ADC=90ºD在RtABD△和RtACD△中证明:作△ABC的高线ADAB=ACAD=AD(公共边)∴Rt△ABD≌Rt△ACD(HL)∴∠B=∠C(全等三角形对应角相等)⒈等腰三角形一个底角为75°,它的另外两个角为_______;⒉等腰三角形一个角为70°,它的另外两个角为___________________;⒊等腰三角形一个角为110°,它的另外两个角为________。75°,30°70°,40°或55°,55°35°,35°小试牛刀想一想想一想::刚才的证明除了能得到∠B=∠C你还能发现什么?重合的线段重合的角ABDCAB=ACBD=CDAD=AD∠B=∠C.∠BAD=∠CAD∠ADB=∠ADC=90°等腰三角形顶角的平分线平分底边并且垂直于底边.性质2(等腰三角形三线合一)ABCD等腰三角形的顶角平分线与底边上的中线,底边上的高互相重合根据等腰三角形性质2,在△ABC中,AB=AC时(1)∵ADBC⊥,∴=,=∠∠(2)∵AD是中线,∴,=⊥∠∠(3)∵AD是角平分线,∴,⊥=BADCADBDCDADBCBADCADADBCBDCD结论:在等腰三角形中,(在ABC中,AB=AC)①∠BAD=CAD∠,②ADBC⊥,③BD=CD中已知任意一个都可以得其它两个条件.ACBD例1、如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。ABCD解:∵AB=AC,BD=BC=AD,∴∠ABC=C=BDC∠∠,∠A=ABD∠(等边对等角)设∠A=x,则∠BDC=A+ABD=2x,∠∠从而∠ABC=C=BDC=2x,∠∠于是在△ABC中,有∠A+ABC+C=x+∠∠2x+2x=180°,解得x=36°,在△ABC中,∠A=36°,∠ABC=C=∠72°x⌒2x⌒2x⌒⌒2x轴对称图形两个底角相等,简称“等边对等角”顶角平分线、底边上的中线、和底边上的高互相重合,简称“三线合一”性质性质11::等腰三角形的两个底角相等等腰三角形的两个底角相等(简称“等边对等角”,前提是在同一个三角形中。)性质性质22::等腰三角形的等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合。(简称“三线合一”,前提是在同一个等腰三角形中。)你的细心加你的耐心等于成功!如图:△ABC中,AB=AC,AD和BE是高,它们相交于点H,且AE=BE。求证:AH=2BDABCDEH证明:∵AB=AC,AD是高,BC=2BD∴⌒1⌒2又∵BE是高,∴∠ADC=BEC=AEH∠∠=90°在△AEH和△BEC中∴△AEHBEC(ASA)≌△∴∠1+C=2+C=90°∠∠∠∴1=2∠∠︸∠AEH=BEC∠AE=BE∠1=2∠∴AH=BC∴AH=2BD思考如图,已知△ABC中,AB=AC,F在AC上,在BA的延长线上截取AE=AF,求证:ED⊥BCABCDEF思考