实际问题与反比例函数()VIP免费

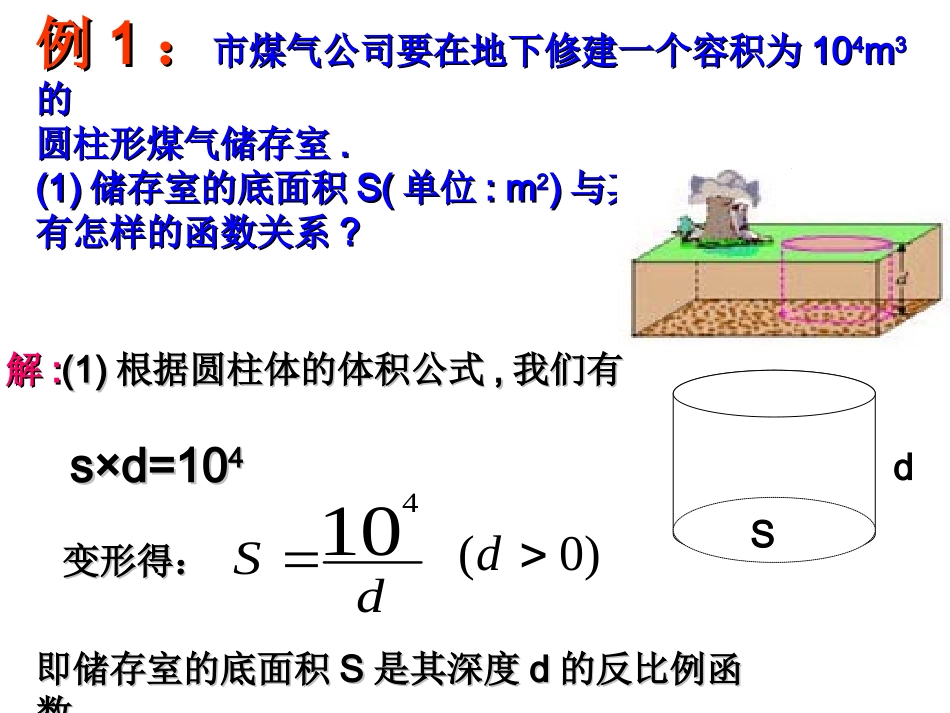
第二十六章反比例函第二十六章反比例函数数例例11：：市煤气公司要在地下修建一个容积为市煤气公司要在地下修建一个容积为101044mm33的的圆柱形煤气储存室圆柱形煤气储存室..(1)(1)储存室的底面积储存室的底面积S(S(单位单位:m:m22))与其深度与其深度d(d(单位单位:m):m)有怎样的函数关系有怎样的函数关系??解解::(1)(1)根据圆柱体的体积公式根据圆柱体的体积公式,,我们有我们有s×d=10s×d=1044变形得：变形得：即储存室的底面积即储存室的底面积SS是其深度是其深度dd的反比例函的反比例函数数..dS104)0(ddS解解::(2)(2)把把S=500S=500代入代入,,得：得：dS104d104500答答::如果把储存室的底面积定为如果把储存室的底面积定为500,500,施工时施工时应向地下掘进应向地下掘进20m20m深深..m2(2)(2)公司决定把储存室的底面积公司决定把储存室的底面积SS定为定为500m500m22,,施施工工队施工时应该向下掘进多深队施工时应该向下掘进多深??20d解得：解得：解解::(3)(3)根据题意根据题意,,把把d=15d=15代入代入,,得：得：dS10415104s解得：解得：S≈666.67S≈666.67答答::当储存室的深为当储存室的深为15m15m时时,,储存室的底面积应改为储存室的底面积应改为666.67666.67才能满足需要才能满足需要..m2(3)(3)当施工队按当施工队按(2)(2)中的计划掘进到地下中的计划掘进到地下15m15m时时,,碰碰上了坚硬的岩石上了坚硬的岩石..为了节约建设资金为了节约建设资金,,储存室的底储存室的底面积应改为多少才能满足需要面积应改为多少才能满足需要((保留两位小数保留两位小数)?)?随堂练习11(1)(1)已知某矩形的面积为已知某矩形的面积为20cm20cm22,,写出其长写出其长yy与宽与宽xx之之间的函数表达式间的函数表达式;;(2)(2)当矩形的长为当矩形的长为12cm12cm是是,,求宽为多少求宽为多少??当矩形的当矩形的宽为宽为4cm,4cm,其长为多少其长为多少??(3)(3)如果要求矩形的长不小于如果要求矩形的长不小于8cm,8cm,其宽至多要多少其宽至多要多少??)0()1(20xyx.5,35)2(cmcmcm25)3(1.某蓄水池的排水管每时排水8m3,6h可将满池水全部排空.(1)蓄水池的容积是多少?解:蓄水池的容积为:8×6=48(m3).(2)如果增加排水管,使每时的排水量达到Q(m3),那么将满池水排空所需的时间t(h)将如何变化?答:此时所需时间t(h)将减少.(3)写出t与Q之间的函数关系式;解:t与Q之间的函数关系式为:Qt48想一想：想一想：1.某蓄水池的排水管每时排水8m3,6h可将满池水全部排空.解:当t=5h时,Q=48/5=9.6m3.所以每时的排水量至少为9.6m3.(5)已知排水管的最大排水量为每时12m3,那么最少多长时间可将满池水全部排空?解:当Q=12(m3)时,t=48/12=4(h).所以最少需4h可将满池水全部排空.(6)画出函数图象,根据图象请对问题(4)和(5)作出直观解释,并和同伴交流.(4)如果准备在5h内将满池水排空,那么每时的排水量至少为多少?例2：码头工人以每天30吨的速度往一艘轮船装载货物，把轮船装载完毕恰好用了8天时间.（1）轮船到达目的地后开始卸货，卸货速度v（单位：吨／天）与卸货时间t（单位：天）之间有怎样的关系？（2）由于遇到紧急情况，船上的货物必须在不超过5日内卸完，那么平均每天至少要卸多少吨货物？分析：（1）根据装货速度×装货时间＝货物的总量，可以求出轮船装载货物的的总量；（2）再根据卸货速度＝货物总量÷卸货时间，得到ｖ与ｔ的函数式。1.某商场出售一批进价为2元的贺卡，在市场营销中发现此商品的日销售单价x元与日销售量y之间有如下关系：（1）根据表中的数据在平面直角坐标系中描出实数对（x,y）的对应点.（2）猜测并确定y与x之间的函数关系式，并画出图象；（3）设经营此贺卡的销售利润为w元，试求出w与x之间的函数关系式，若物价局规定此贺卡的销售价最高不能超过10元／个，请你求出当日销售单价x定为多少元时，才能获得最大日销售利润？X（元）3456Y（个）201512102.一辆汽车往返于甲、乙两地之间，如果汽车以50千米／时的平均速度从甲地出发，则经过6小时可达到乙地.（1）甲、乙两地相距多少千米？（2）如果汽车把速度提高到v（千米／时），那么从甲地到乙地所用时间t（小时）将怎样变化？（3）写出t与v之间的函...