船有触礁的危险吗VIP免费

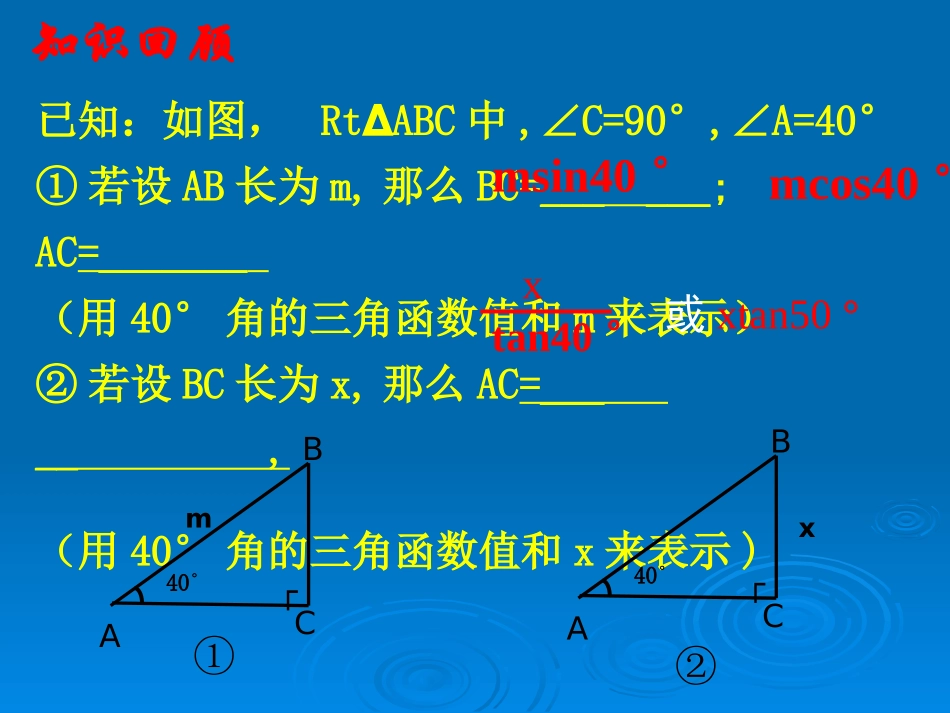
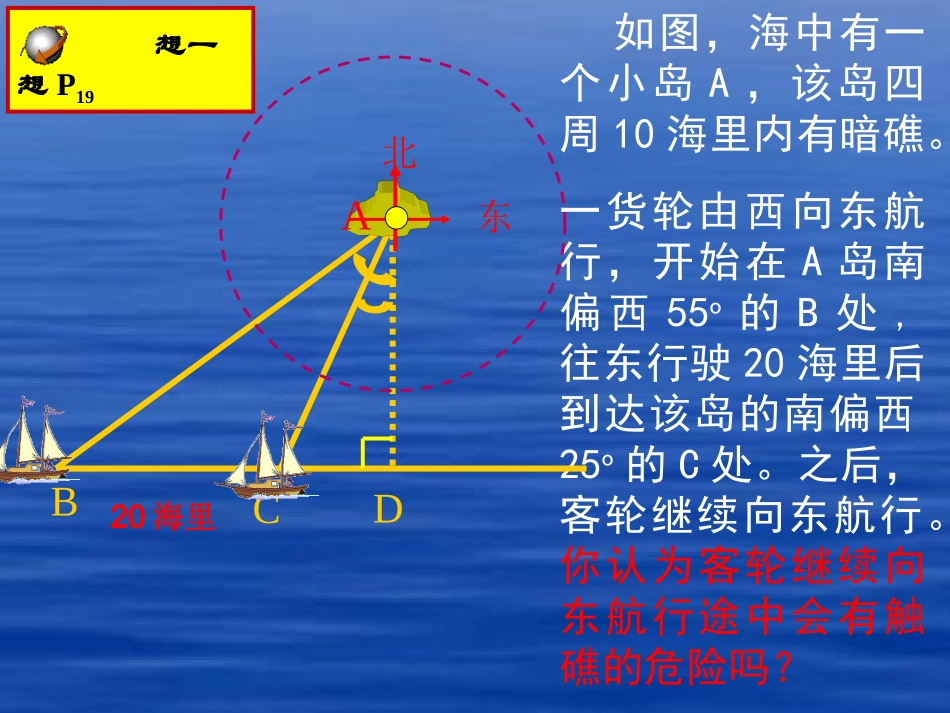
知识回顾已知：如图，RtABC∆中,∠C=90°,∠A=40°①若设AB长为m,那么BC=______;AC=_______（用40°角的三角函数值和m来表示）②若设BC长为x,那么AC=_____,（用40°角的三角函数值和x来表示)ABC┌40°m①ABC┌40°x②msin40°mcos40°xtan40°或xtan50°如图，海中有一个小岛A，该岛四周10海里内有暗礁。一货轮由西向东航行，开始在A岛南偏西55o的B处,往东行驶20海里后到达该岛的南偏西25o的C处。之后，客轮继续向东航行。你认为客轮继续向东航行途中会有触礁的危险吗？BCD小小航海家东北A想一想P1920海里解：如图,由题可得：在RtABD∆和RtACD∆中∠BAD=55°,∠CAD=25°,BC=20海里.答:货轮继续向东航行途中没有触礁的危险.DABC,25tan,55tanxCDxBD.25tan,55tanxCDxBD55°25°.2025tan55tanxx25tan55tan20x分析:要知道货轮继续向东航行途中有无触礁的危险,只要过点A作AD⊥BC，垂足为D,如果AD>10海里,则无触礁的危险.1079.204663.04281.120设AD为x海里.20海里如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至B处,测得仰角为60°,那么该塔有多高?(小明的身高忽略不计,结果精确到1m).想一想P19要解决这问题,我们仍需将其数学化.请与同伴交流你是怎么想的?准备怎么去做?现在你能完成这个任务吗?古塔究竟有多高DABC┌50m30°60°,tan,tanxBCBDCxACADC.30tan,60tanxBCxAC.5030tan60tanxx.433253335030tan60tan50mx答:该塔约有43m高.解:如图,RtACD∆和Rt∆BCD中∠A=30°,∠DBC=60°,AB=50m,则∠ADC=60°,∠BDC=30°,设CD=xm.问题解决某商场准备改善原有楼梯的安全性能,把倾斜角由原来的40°减至35°,已知原楼梯的长度为4m,调整后的楼梯会加长多少?楼梯多占多长一段地面?(结果精确到0.01m).做一做P22ABCD┌楼梯加长了多少解:如图,在RtABC∆和Rt∆BCD中,∠A=35°,∠BDC=40°,DB=4m.ABCD┌4m35°40°,40sinBDBC.40sinBDBC,35sinABBC答:调整后的楼梯会加长约0.48m..48.45736.06428.0435sin40sin35sinmBDBCAB.48.0448.4mBDAB问题解决求AB—BD和AD的长解:如图,RtABD∆和RtACD中,∠A=35°,∠BDC=40°,DB=4m.ABCD┌4m35°40°,40tanDCBC.40tanBCDC,35tanACBC答:楼梯多占约0.61m长的一段地面..35tanBCACDCACAD40tan135tan1BC40tan135tan140sinBD.61.0m问题解决55°25°ABCD┌4m35°40°DABC┌50m30°60°ABCD总结归纳20海里1.审题将生活问题数学化，即画出符合题意的示意图归纳总结2.找直角三角形或构造直角三角形，利用三角函数中的边角关系解决问题如图,一灯柱AB被一钢缆CD固定.CD与地面成40°夹角,且DB=5m.现再在C点上方2m处加固另一根钢缆ED,那么,钢缆ED的长度为多少?(结果精确到0.01m).随堂练习P20EBCD2m40°5m钢缆长几何独立作业P24习题1.61,2,3题;祝你成功！知识的升华下课了!结束寄语•悟性的高低取决于有无悟“心”,其实,人与人的差别就在于你是否去思考、去发现.解:如图,(2)如果坝长100m,那么修建这个大坝共需多少土石方?(结果精确到0.01m3)再求体积!先算面积!,2得由梯形面积公式AFBCADS答:修建这个大坝共需土石方约10182.34m3..27222436S.34.101822721001003mSV100mABCD6m30mF┌计算需要空间想象力问题解决