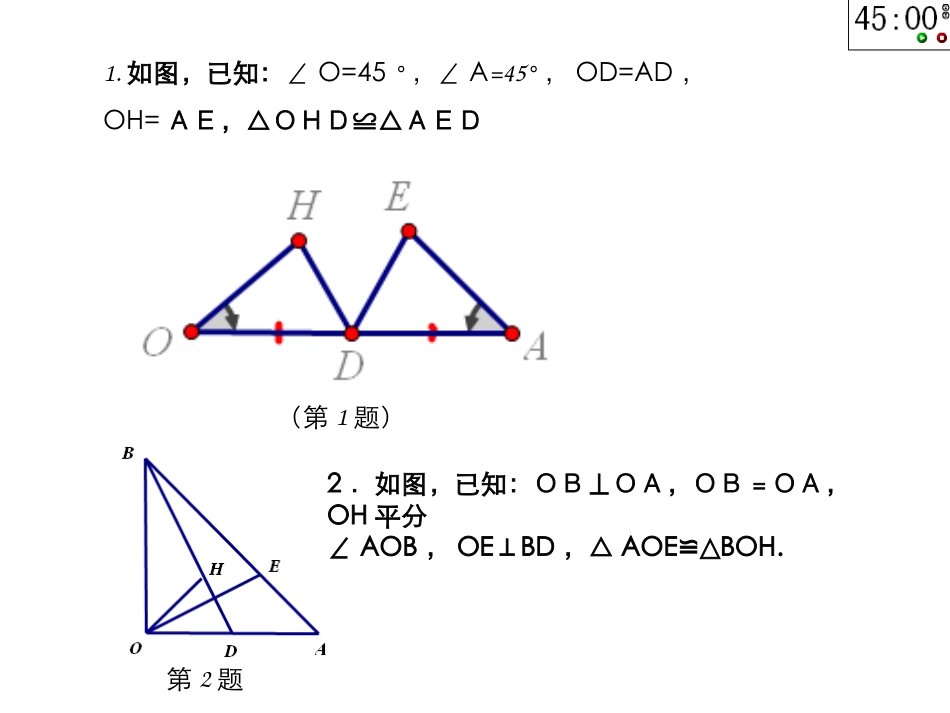
难题其实很简单新林中学——常光发校内公开课2011.11.101.如图,已知:∠O=45°,∠A=45°,OD=AD,OH=AE,△OHD≌△AED(第1题)第2题2.如图,已知:OB⊥OA,OB=OA,OH平分∠AOB,OE⊥BD,△AOE≌△BOH.xyBDGAO3.如图,OA=OB,GA⊥OX,OG⊥BD.求证:OD=AG.(第3题)GFAD(第4题)4.如图,∠DAF=45°,DA⊥GA,DA=GA.求证:△AFD≌△AFG.5.如图,OB⊥ON,MN⊥ON,△BPM是等腰直角三角形.求证:△BOP≌△PNM.第5题第6题思考:6.如图,P为x轴上A点右侧任意一点,以BP为边作等腰Rt△PBM,其中PB=PM,直线MA交y轴于点Q,当点P在x轴上运动时,线段OQ的长是否发生变化?对于该问题若求出OQ的式子中含有x,那么你认为OQ的长会发生变化吗?若求出OQ的式子中不含有x,那么你认为OQ的长会发生变化吗?24.(12分)如图,直线AB交x轴正半轴于点A(a,0),交y轴正半轴于点B(0,b),且a、b满足+|4-b|=0,(1)求A、B两点的坐标;(2)D为OA的中点,连接BD,过点O作OE⊥BD于F,交AB于E,求证∠BDO=∠EDA;(3)如图,P为x轴上A点右侧任意一点,以BP为边作等腰Rt△PBM,其中PB=PM,直线MA交y轴于点Q,当点P在x轴上运动时,线段OQ的长是否发生变化?若不变,求其值;若变化,求线段OQ的取值范围.NoImage4a(2)有其他方法吗H你如何拆分原题?:自主纠正试卷中的错误解后反思:(1)本题考查的是算术平方根和绝对值的性质.(2)本题灵活考查的是全等三角形的判定与性质及特殊三角形的性质.(3)综合运用知识进行计算与推理是解此题的关键.难题都是由简单题组成的,看来基础知识不能忽视!更重要的是要善于将复杂的问题拆分成几个简单的问题加以解决.