随机变量的数字特征与正态分布课件VIP免费

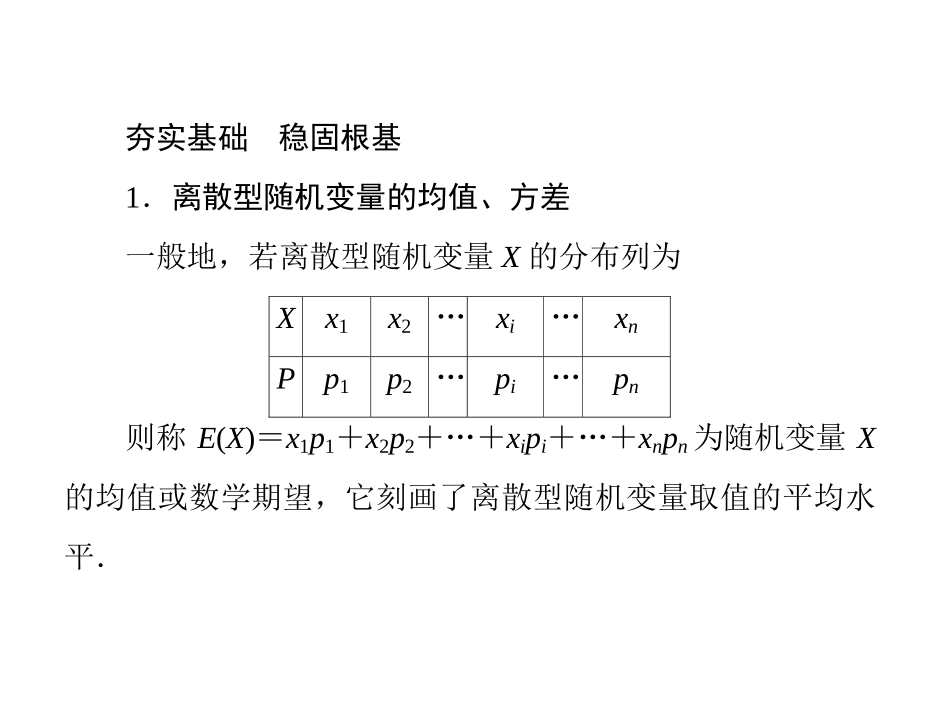
第十章第九节随机变量的数字特征与正态分布泰安二中数学泰安二中数学**重点难点引领方向重点：掌握随机变量的期望、方差和正态分布的概念．难点：随机变量的期望与方差的意义、正态曲线的性质．基础梳理导学夯实基础稳固根基1．离散型随机变量的均值、方差一般地，若离散型随机变量X的分布列为Xx1x2…xi…xnPp1p2…pi…pn则称E(X)＝x1p1＋x2p2＋…＋xipi＋…＋xnpn为随机变量X的均值或数学期望，它刻画了离散型随机变量取值的平均水平．称D(X)＝i＝1n(xi－E(X))2pi为随机变量X的方差，其算术平方根DX为随机变量X的标准差．方差和标准差刻画了随机变量取值的稳定与波动、集中与离散的程度．(1)若Y＝aX＋b，其中a、b为常数，则Y也是随机变量．P(Y)＝P(aX＋b)＝P(X＝xi)，i＝1,2，…，n，E(Y)＝E(aX＋b)＝aE(X)＋b.D(Y)＝D(aX＋b)＝a2D(X)．(2)D(X)＝E(X－E(X))2.2．两点分布、二项分布、超几何分布的均值、方差(1)若X服从两点分布，则E(X)＝p，D(X)＝．(2)若X～B(n，p)，则E(X)＝np，D(X)＝．※(3)若X服从参数为N、M、n的超几何分布，则E(X)＝nMN.p(1－p)np(1－p)3．正态分布(1)正态曲线函数f(x)＝φμ，σ(x)＝12πσe－（x－μ）22σ2，x∈R.其中实数μ和σ为参数，我们称f(x)的图象为正态曲线．服从正态分布的随机变量叫做正态变量．正态随机变量X落在区间[a，b]内的概率为：P(a0，有P(μ－a