信息论基础——信源编码VIP免费

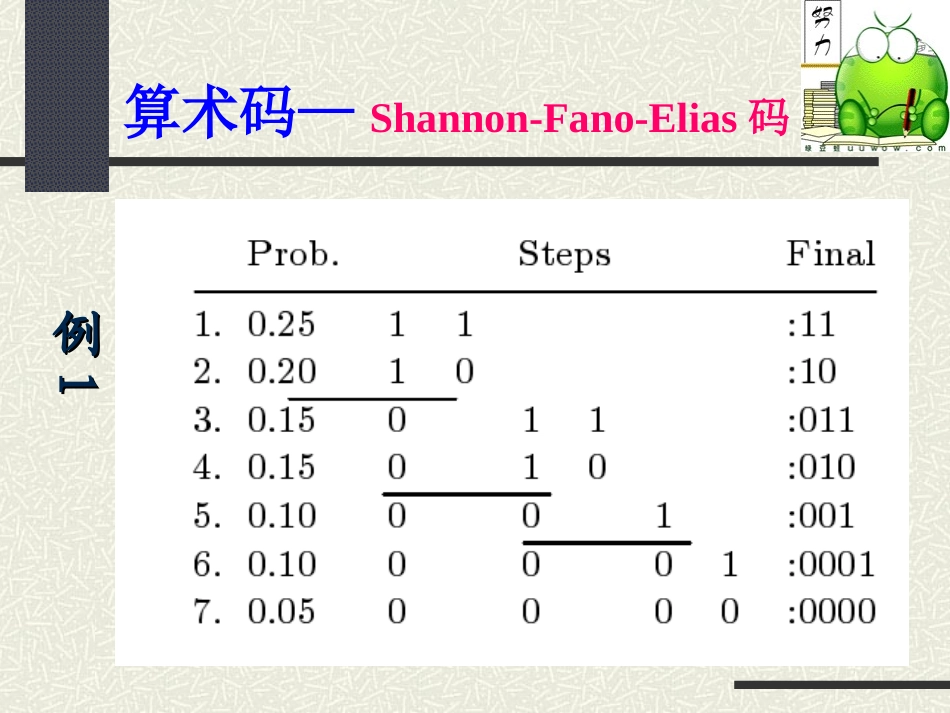
数据压缩和信源编码3.1等长码3.2变长编码3.3哈夫曼码3.4算术码香农-费诺码3.5通用信源编码LZW算法习题三0.概述是第一个能够找到的好的变长码.原则：按照符号出现的概率从大到小排序，然后将其分成两个出现概率相同或几乎相同的子集—一个子集的编码均以0打头，另一个子集的编码均以1打头；然后把每个子集再分成两个更小的子集，同样确定所有码字的第二位，依次循环.算术码—Shannon-Fano-Elias码算术码—Shannon-Fano-Elias码例例110.概述平均码长：0.25×2+0.20×2+0.15×3+0.15×3+0.10×3+0.10×4+0.05×4=2.7bits/symbol.熵：-（0.25log0.25+0.20log0.20+0.15log0.15+0.15log0.15+0.10log0.10+0.10log0.10+0.05log0.05≈2.67.这是一个较好的结果！算术码—Shannon-Fano-Elias码算术码—Shannon-Fano-Elias码例例22算术码—Shannon-Fano-Elias码12,13,44xx例例331.基本思路用二进制小数表示信源的概率分布，如果概率分布取值大，则它的二进制位数就低；另外，为了使算术码具有前缀性（无尾随后缀），对概率分布采用累计求和计算.算术码—Shannon-Fano-Elias码2.编码方法1）将信源符号X={a1,a2,……,aq}依次排列（不要求以概率大小排序）；2）计算各符号的修正累积分函数值3）确定各信源符号所对应码字的码长4）将F(ak)表示为二进制小数，并用小数点后的l(ak)位作为ak的码字.<若后面有尾数，要进位>111()()()2kkikiFxapapa1()log1()kklapa算术码—Shannon-Fano-Elias码[x]代表不小于x的整数若二进制小数后面有尾数，则截断例1：若信源的概率分布为若信源的概率分布为，取信，取信号字母表为，求信源的算号字母表为，求信源的算术码术码..12,13,44xx0,1U算术码—Shannon-Fano-Elias码例1：若信源的概率分布为若信源的概率分布为，取信，取信号字母表为，求信源的算号字母表为，求信源的算术码术码..12,13,44xx0,1U算术码—Shannon-Fano-Elias码11211()()0.125(0.)28001Fxpx212215()()()0.6125(0.80)2Fxpxpx例1：若信源的概率分布为若信源的概率分布为，取信，取信号字母表为，求信源的算号字母表为，求信源的算术码术码..12,13,44xx0,1U算术码—Shannon-Fano-Elias码10例2有一单符号离散无记忆信源对该信源编二进制香农-费诺码.其编码过程如下表所示：123456,,,,,()0.250.250.200.150.100.05XxxxxxxPX算术码—Shannon-Fano-Elias码二进制香农编码xip(xi)pa(xj)li码字x10.250.1253001(0.001)2x20.250.3753011(0.011)2x30.200.6041001(0.10011)2x40.150.77541100(0.110001)2x50.100.905111001(0.1110011)2x60.050.9756111110(0.1111100)2算术码—Shannon-Fano-Elias码计算出给定信源香农码的平均码长若对上述信源采用等长编码，要做到无失真译码，每个符号至少要用3个比特表示。相比较，香农编码对信源进行了压缩。由离散无记忆信源熵定义，可计算出：对上述信源采用香农编码的信息率为编码效率为信源熵和信息率之比。则可以看出，编码效率并不是很高。0.2522(0.20.15)30.1040.0552.7(/)L比特符号222.7loglog22.71,21LRmLmL这里()2.4289.63%2.7HXR621()()log()2.42(/)iiiHXpxpx比特符号算术码—Shannon-Fano-Elias码•思考（一）：用Shannon-Fano-Elias码方法将信源编成二元变长唯一可译码，并计算其码率.1234567()0.200.190.180.170.150.100.01Xaaaaaaapx算术码—Shannon-Fano-Elias码算术码—Shannon-Fano-Elias码•思考（二）：有两个信源X和Y如下：1)分别用霍夫曼码编成二元变长惟一可译码，并计算其编码效率。*)用Shannon-Fano码编成二元变长惟一可译码•思考（二）：有两个信源X和Y如下：2)分别用Shannon-Fano-Elias编码法编成二元变长惟一可泽码．并计算编码效率.3)从X，Y两种不同信源来比较这三种编码方法的优缺点算术码—Shannon-Fano-Elias码•思考（二）：信源X的二元霍夫曼编码：算术码—Shan...