二维随机变量及其分布函数VIP免费

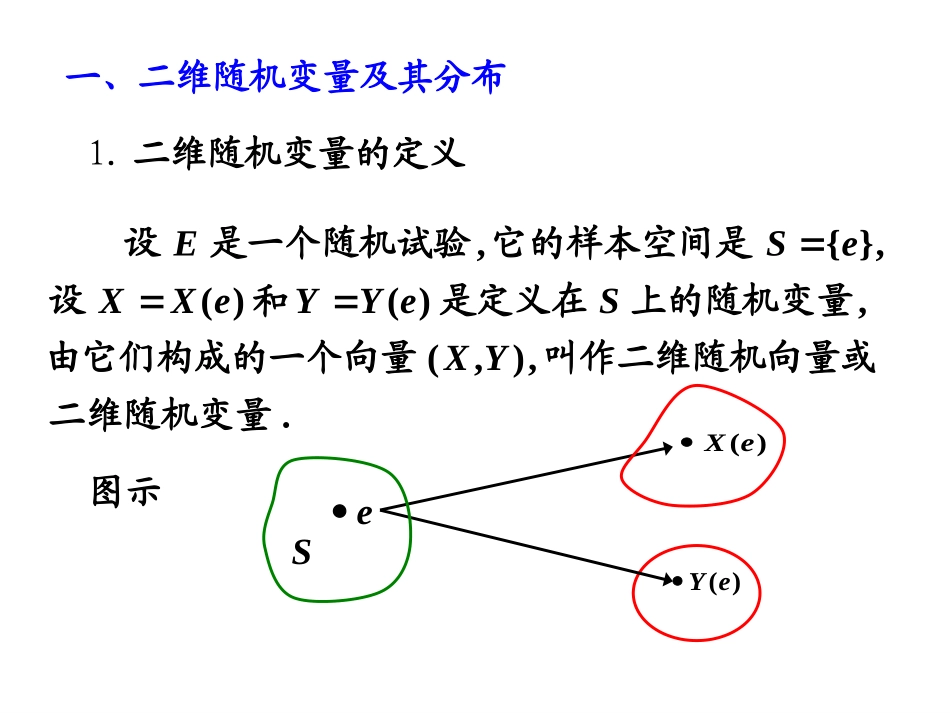
3.1二维随机变量及其分布一.二维随机变量及其分布函数二.二维离散型随机变量及其分布三.二维连续型随机变量及其分布图示e)(eYS)(eX.,),(,)()(,}{,二维随机变量叫作二维随机向量或由它们构成的一个向量上的随机变量是定义在和设它的样本空间是是一个随机试验设YXSeYYeXXeSE一、二维随机变量及其分布1.二维随机变量的定义实例1炮弹的弹着点的位置(X,Y)就是一个二维随机变量.二维随机变量(X,Y)的性质不仅与X、Y有关,而且还依赖于这两个随机变量的相互关系.实例2考查某一地区学前儿童的发育情况,则儿童的身高H和体重W就构成二维随机变量(H,W).说明2.分布函数的定义.,),(},{)}(){(),(:,,,),(的联合分布函数和量或称为随机变的分布函数称为二维随机变量二元函数对于任意实数是二维随机变量设YXYXyYxXPyYxXPyxFyxYXxOy),(yxyYxX,.),(内的概率在如图所示区域的函数值就是随机点落yxF3.分布函数的性质),,(),(,,),(11212oyxFyxFxxyyxyxF时当意固定的即对于任的不减函数和是变量).,(),(,1212yxFyxFyyx时当对于任意固定的,1),(02oyxF,y对于任意固定的,0),(lim),(yxFyFx且有,x对于任意固定的,0),(lim),(yxFxFy.1),(lim),(yxFFyx.,),(,)0,(),(,),0(),(3o也右连续关于右连续关于即yxyxFyxFyxFyxFyxF,0),(lim),(yxFFyx,,),,(),,(421212211oyyxxyxyx对于任意.0),(),(),(),(21111222yxFyxFyxFyxF有证明},{2121yYyxXxP,0},{212yYyxXP},{22yYxXP.0),(),(),(),(21111222yxFyxFyxFyxF故},{211yYyxXP},{12yYxXP},{21yYxXP},{11yYxXP二维离散型随机变量及其分布：分布律、分布函数4.二维随机变量的分类二维连续型随机变量及其分布：分布密度、分布函数若二维随机变量(X,Y)所取的可能值是有限对或无限可列多对,则称(X,Y)为二维离散型随机变量.1.定义2.二维离散型随机变量的分布律.,),(,,2,1,,},{,,2,1,),,(),(的联合分布律和或随机变量的分布律变量称此为二维离散型随机记值为所有可能取的设二维离散型随机变量YXYXjipyYxXPjiyxYXijjiji二、二维离散型随机变量及其分布二维随机变量(X,Y)的分布律也可表示为.1,011ijijijpp其中(,)ijijPXxYypXYjyyy21ixxx21111212122212jjiiijppppppppp.),(.~1,4,3,2,1的分布律试求整数值中等可能地取一在另一个随机变量取值四个整数中等可能地在设随机变量YXXYX解:},{的取值情况是jYiX,4,3,2,1i.的正整数取不大于ij且由乘法公式得},{jYiXP}{}{iXPiXjYP,411i,4,3,2,1i.ij的分布律为于是),(YX例1XY12341234418112116108112116100121161000161(X,Y)所取的可能值是),0,0(解),1,0(),0,1(),1,1(),2,0().0,2(}0,0{YXP,28328230203抽取两支都是绿笔抽取一支绿笔,一支红笔例2从一个装有3支蓝色、2支红色、3支绿色圆珠笔的盒子里,随机抽取两支,若X、Y分别表示抽出的蓝笔数和红笔数,求(X,Y)的分布律.}1,0{YXP,14328131203}2,0{YXP}0,1{YXP}0,2{YXP}1,1{YXP,14328031213,28128032203,28928130213.28328030223故所求分布律为XY210283289283143143028100012例3一个袋中有三个球,依次标有数字1,2,2,从中任取一个,不放回袋中,再任取一个,设每次取球时,各球被取到的可能性相等,以X,Y分别记第一次和第二次取到的球上标有的数字,求(X,Y)的分布律与分布函数.(X,Y)的可能取为),2,1(,312231}2,1{YXP,312132}1,2{YXP.312132}2,2{YXP解),1,2().2,2(故(X,Y)的分布为XY21213103131,31,0222112...