专题二次函数中的动点问题2平行四边形存在性问题VIP免费

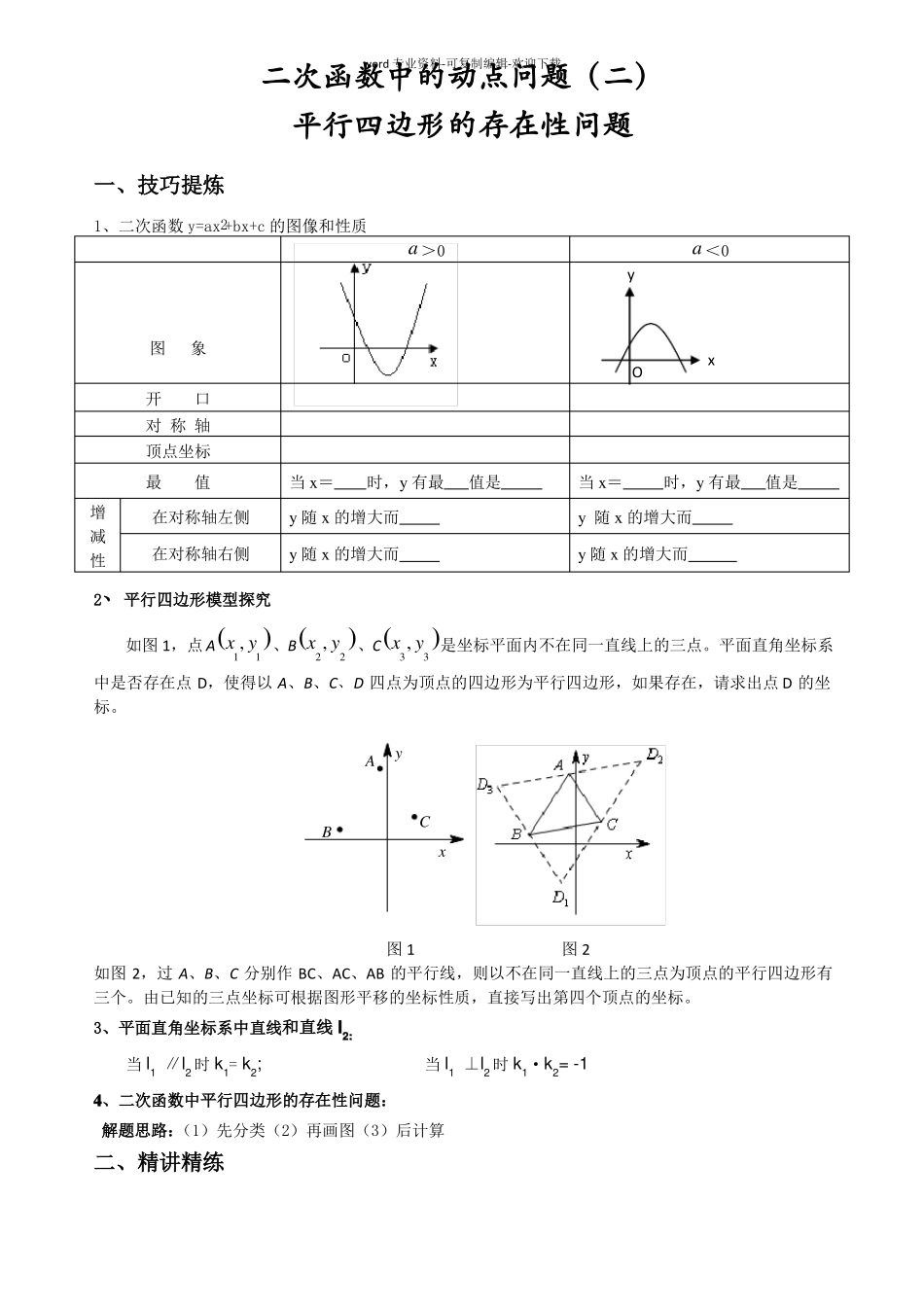
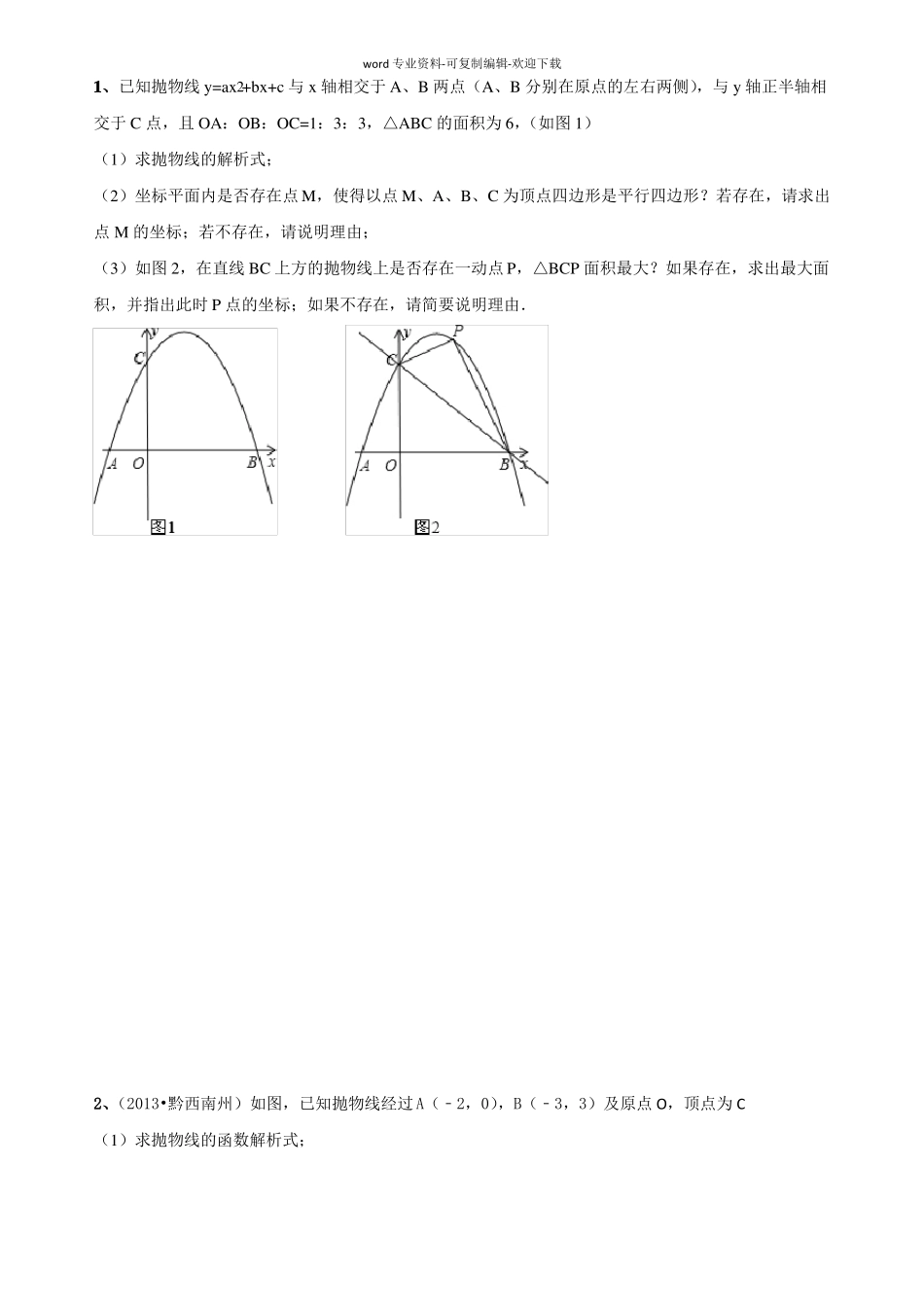
word专业资料-可复制编辑-欢迎下载二次函数中的动点问题（二）平行四边形的存在性问题一、技巧提炼1、二次函数y=ax+bx+c的图像和性质图象开口对称轴顶点坐标最值增减性在对称轴左侧在对称轴右侧2a＞0当x＝时，y有最值是y随x的增大而y随x的增大而ya＜0x当x＝时，y有最值是y随x的增大而y随x的增大而O2、平行四边形模型探究如图1，点Ax1,y1、Bx2,y2、Cx3,y3是坐标平面内不在同一直线上的三点。平面直角坐标系中是否存在点D，使得以A、B、C、D四点为顶点的四边形为平行四边形，如果存在，请求出点D的坐标。AyBCx图1图2如图2，过A、B、C分别作BC、AC、AB的平行线，则以不在同一直线上的三点为顶点的平行四边形有三个。由已知的三点坐标可根据图形平移的坐标性质，直接写出第四个顶点的坐标。3、平面直角坐标系中直线和直线l2:当l1∥l2时k1=k2;当l1⊥l2时k1·k2=-14、二次函数中平行四边形的存在性问题：解题思路：（1）先分类（2）再画图（3）后计算二、精讲精练word专业资料-可复制编辑-欢迎下载1、已知抛物线y=ax2+bx+c与x轴相交于A、B两点（A、B分别在原点的左右两侧），与y轴正半轴相交于C点，且OA：OB：OC=1：3：3，△ABC的面积为6，（如图1）（1）求抛物线的解析式；（2）坐标平面内是否存在点M，使得以点M、A、B、C为顶点四边形是平行四边形？若存在，请求出点M的坐标；若不存在，请说明理由；（3）如图2，在直线BC上方的抛物线上是否存在一动点P，△BCP面积最大？如果存在，求出最大面积，并指出此时P点的坐标；如果不存在，请简要说明理由．2、（2013•黔西南州）如图，已知抛物线经过A（﹣2，0），B（﹣3，3）及原点O，顶点为C（1）求抛物线的函数解析式；word专业资料-可复制编辑-欢迎下载（2）设点D在抛物线上，点E在抛物线的对称轴上，且以AO为边的四边形AODE是平行四边形，求点D的坐标。【变式练习】（2007•河南）如图，对称轴为直线x=7的抛物线经过点A（6，0）和B（0，4）．2（1）求抛物线解析式及顶点坐标；（2）设点E（x，y）是抛物线上一动点，且位于第四象限，四边形OEAF是以OA为对角线的平行四边形，word专业资料-可复制编辑-欢迎下载求平行四边形OEAF的面积S与x之间的函数关系式，并写出自变量x的取值范围；①当平行四边形OEAF的面积为24时，请判断平行四边形OEAF是否为菱形？②是否存在点E，使平行四边形OEAF为正方形？若存在，求出点E的坐标；若不存在，请说明理由．四、方法规律1、平行四边形模型探究如图1，点Ax1,y1、Bx2,y2、Cx3,y3是坐标平面内不在同一直线上的三点。平面直角坐标系中是否存在点D，使得以A、B、C、D四点为顶点的四边形为平行四边形，如果存在，请求出点D的坐标。word专业资料-可复制编辑-欢迎下载AyBCx图1图2以不在同一直线上的三点为顶点的平行四边形有三个。由已知的三点坐标可根据图形平移的坐标性质，直接写出第四个顶点的坐标。2、平面直角坐标系中直线和直线l2:当l1∥l2时k1=k2;当l1⊥l2时k1·k2=-1五、实战训练1、抛物线y＝－(x＋2)2－3的顶点坐标是（）(A)（2，－3）；(B)（－2，3）；(C)（2，3）；(D)（－2，－3）2、已知抛物线yax2bxca0在平面直角坐标系中的位置如图所示，则下列结论中，正确的是（）A、a＞0B、b＜0C、c＜0D、a+b+c＞03、函数yax2a0与yax2a0在同一平面直角坐标系中的图象可能是（）4、如图，一次函数y1kxn(k0)与二次函数y2axbxc(a0)的图象相交于A(1，5)、B(9，2)两点，则关于x的不等式kxnaxbxc的解集为（）A、1x9B、1x9C、1x9D、x1或x922word专业资料-可复制编辑-欢迎下载5、出售某种手工艺品，若每个获利x元，一天可售出(8x)个，则当x为多少元，一天出售该种手工艺品的总利润y最大。6、（2012•宜宾）如图，抛物线y=x﹣2x+c的顶点A在直线l：y=x﹣5上。（1）求抛物线顶点A的坐标；（2）设抛物线与y轴交于点B，与x轴交于点C．D（C点在D点的左侧），试判断△ABD的形状；（3）在直线l上是否存在一点P，使以点P、A、B、D为顶点的四边形是平行四边形？若存在，求点P的坐标；若不存在，请说明理由。27、已知...