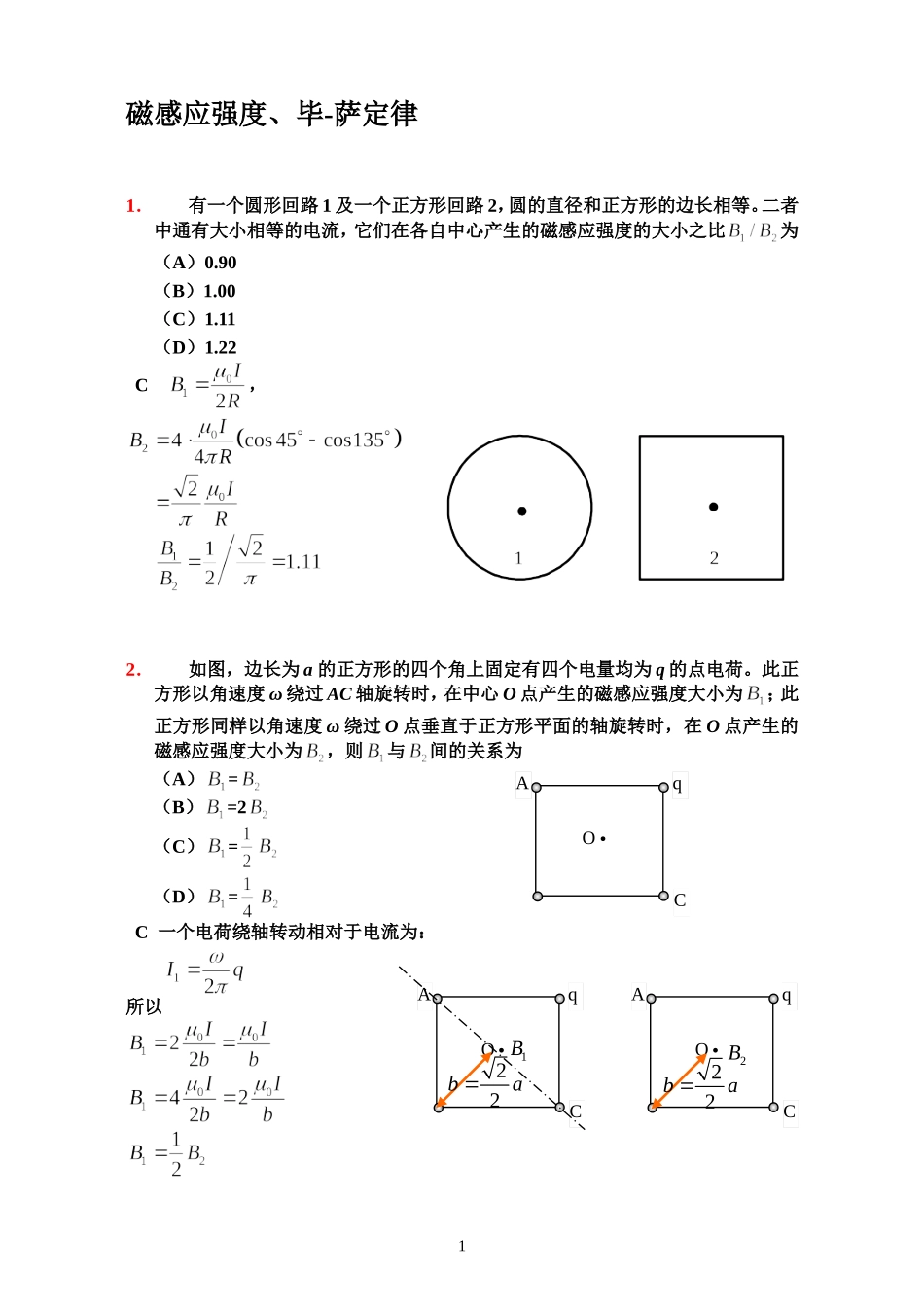
磁感应强度、毕-萨定律1.有一个圆形回路1及一个正方形回路2,圆的直径和正方形的边长相等。二者中通有大小相等的电流,它们在各自中心产生的磁感应强度的大小之比为(A)0.90(B)1.00(C)1.11(D)1.22C,2.如图,边长为a的正方形的四个角上固定有四个电量均为q的点电荷。此正方形以角速度ω绕过AC轴旋转时,在中心O点产生的磁感应强度大小为;此正方形同样以角速度ω绕过O点垂直于正方形平面的轴旋转时,在O点产生的磁感应强度大小为,则与间的关系为(A)=(B)=2(C)=(D)=C一个电荷绕轴转动相对于电流为:所以1C.AOqC.AOq1B22baC.AOq2B22ba4.在xy平面内有两根互相绝缘、分别通有电流和的长直导线,设两导线互相垂直(如图),则在xy平面内磁感应强度为零的点的轨迹方程为。解:经分析,在xy平面内磁感应强度为零的点的轨迹应该在I、III象限,无限长载流直导线所产生的磁感应强度公式为:所以有,5.均匀带电直线AB,电荷线密度为,绕垂直于直线的轴O以角速度ω匀速转动(线的形状不变,O点在AB延长线上),求:(1)O点的磁感应强度B,(2)磁矩,(3)若a>>b,求及。解:(1)对一段,电荷,旋转形成圆电流,则,它在O点的磁感应强度(2)(3)若,则,过渡到点电荷的情况,B的方向在λ>0时为垂直圈面向后,同理在a>>b时,则也与点电荷运动后的磁矩相同。6.如图,半径为a,带正电荷且线密度为的半圆,以角速度ω绕轴匀速旋转,求:2yIx(1)O点的,(2)旋转的带电半圆的磁矩。(积分公式)解:(1)对弧元,旋转形成圆电流它在O点的磁感应强度为(此处应用圆环形电流在轴线上产生场强大小的公式,公式里的在此处的问题里为,为)方向向上。方向向上。7.一半径为R的带电塑料圆盘,其中有一半径为r的阴影部分均匀带正电荷,面密度为+,其余部分均匀带负电荷,面密度为-。当圆盘以角速度ω旋转时,测得圆盘中心O点的磁感应强度为零,R与r满足什么关系?解:带电圆盘旋转可视为无数电流圆环,取半径为ρ,宽为的电流圆环,在O点的磁场,而故正电部分产生的磁感应强度负电部分产生的磁感应强度由于,所以。3安培环路定律、运动电荷的磁场9.如图,两根直导线ab和cd沿半径方向被接到一个截面处处相等的铁环上,稳恒电流I从a端流入而从d端流出,则磁感应强度B沿图中闭合路径L的积分等于(A)(B)(C)/4(D)2/3D大弧bc流过的电流为,小弧bc流过的电流为,根据安培环路定理有10.在图(a)和(b)中各有一半径相同的圆形回路、,圆周内有电流、,其分布相同,且均在真空中,但在(b)图中回路外有电流,、为两圆形回路上的对应点,则(A),(B),(C),(D),C根据安培环路定理。13.一根半径为R的长直导线载有电流I,做一宽为R,长为L的假想平面S,如图所示。若假想平面S可在导线直径与轴OO’所定的平面内离开OO’轴移动至远处,试求当通过S面的磁通量最大时S面的位置(设直导线内电流分布是均匀的)。.解:设x为假想平面上与对称轴近的一边与对称中心轴线的距离,则4其中(导线内),(导线外)故令,得14.有一无限长圆柱形导体和一无限长薄圆桶形导体,都通有沿轴向均匀分布的电流I,它们的磁导率都为,外半径都为R。今取长L、宽为2R的矩形平面ABCD和A’B’C’D’,AD及A’D’正好在圆柱的轴线上,如图所示,问通过ABCD的磁通量为多少?通过A’B’C’D’的磁通量为多少?解:圆柱形载流导体在空间的磁感应强度的分布为();()穿过ABCD的φ为圆筒载流导线在空间的磁感应强度分布();()15.两平行长直导线相距d=40cm,每根导线载有电流,如图,求:(1)两导线所在平面内与该两导线等距的一点A处的磁感应强度,(2)通过图中斜线所示面积的磁通量(,)。.解:两导线所在平面内,两导线之间任一点P处,和产生的和同方向(均为垂直纸面向外)。所以P点的磁感应强度的大小为设P点距导线1为x,则,5(1)在离两线等距离处的A点,,=故(2)通过图中斜线所示面积的磁通量?16.电流均匀地流过无限大平面导体薄板,单位宽度的电流密度为,设板的厚度可以不计,试求板外任一点的磁感应强度。解法一:用安培环路定理,这是一种方便的解法,在课堂例题中已经讲...