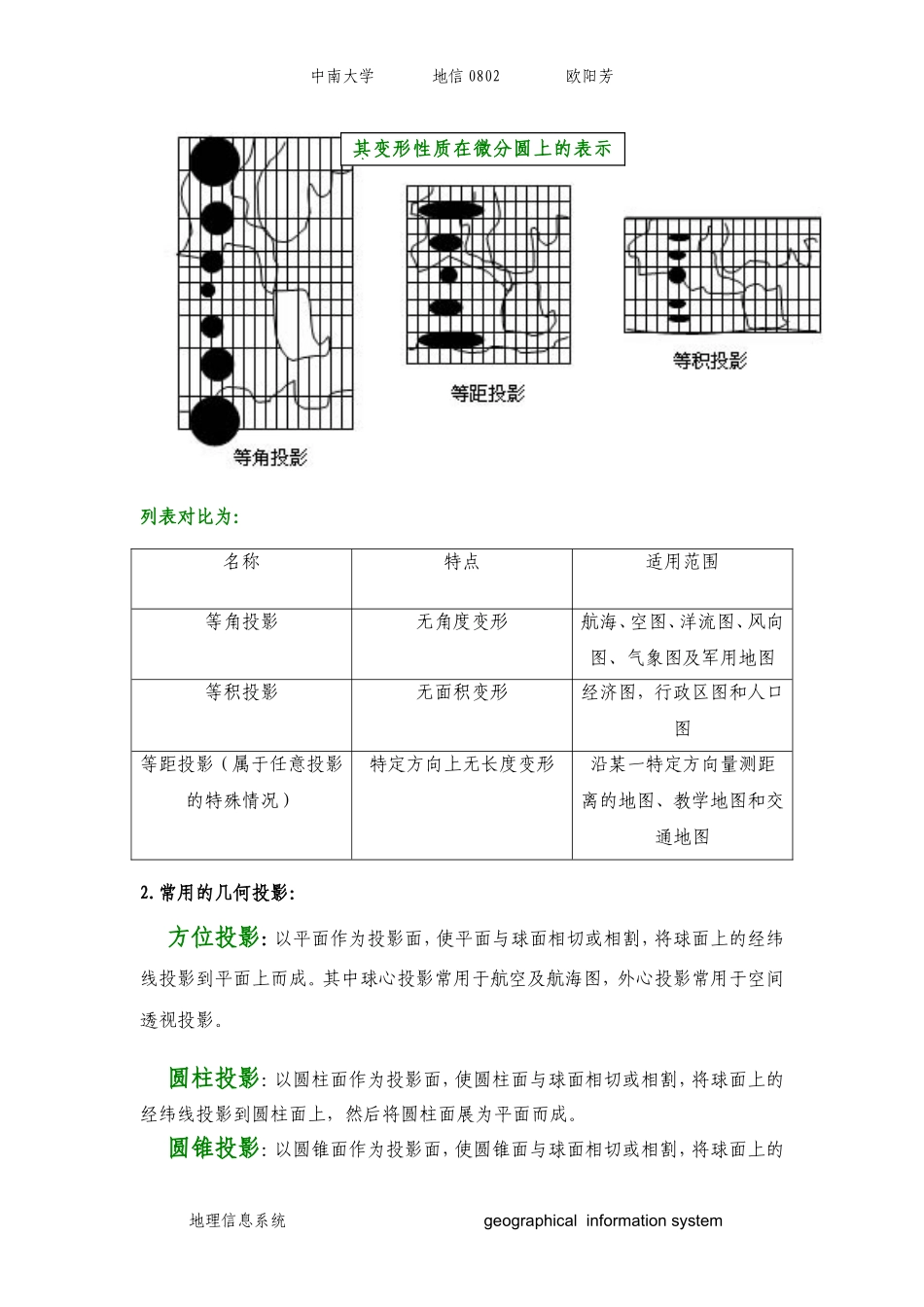
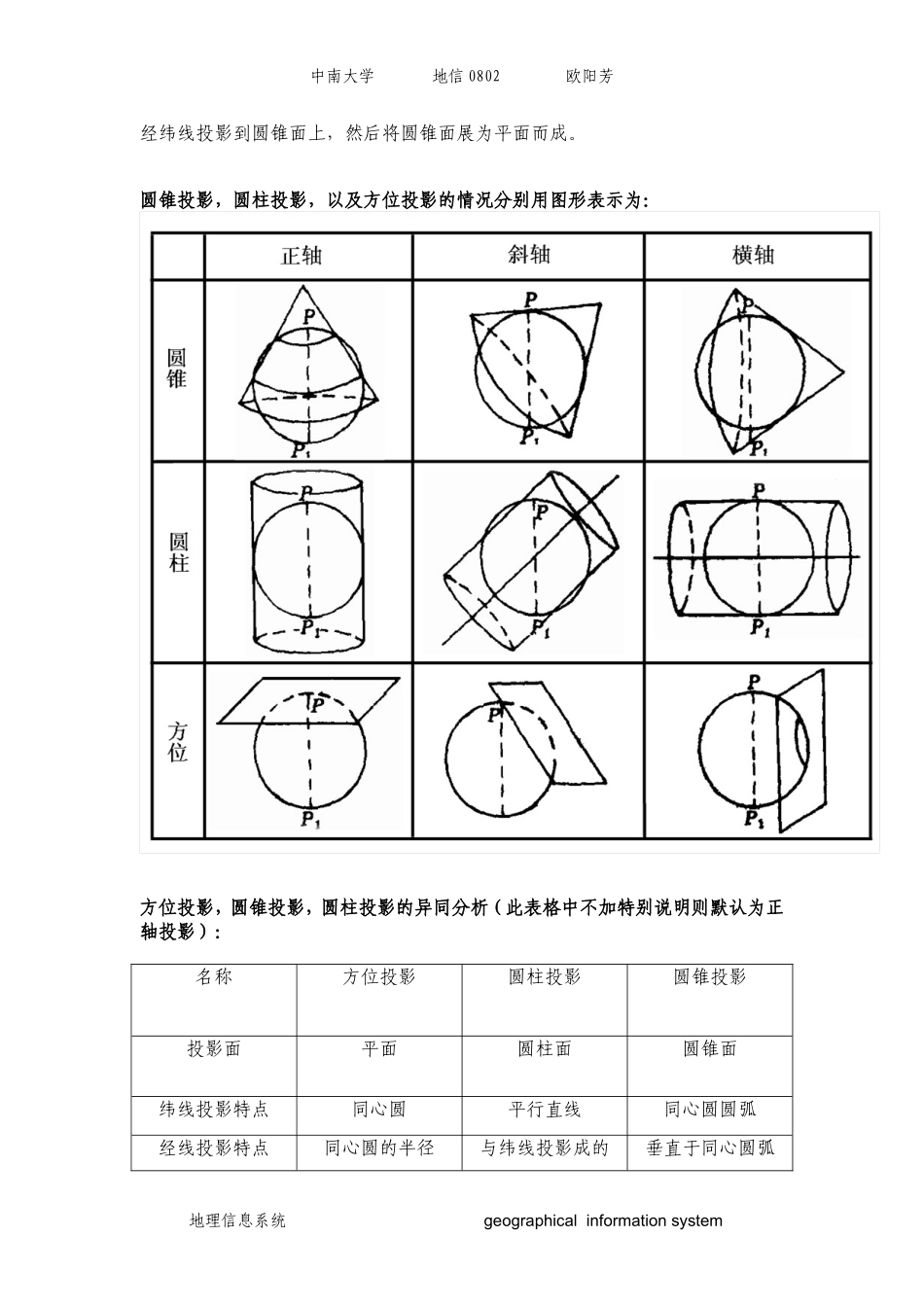
中南大学地信0802欧阳芳常见地图投影欧阳芳地图投影:按变形性质分类:等角投影,等积投影,任意投影按几何构成方法分类:方位投影,圆柱投影,圆锥投影按非几何构成方法分类:伪方位投影,伪圆柱投影,伪圆锥投影,多圆锥投影按照投影面积与地球相割或相切分类:割投影,切投影这里只介绍常见常用的地图投影。1.常见的地图投影按变形性质分为:等角投影:定义为投影前后对应的微分面积保持图形相似,即角度变形为零,也称正形投影。其在一点上任意方向的长度比都相等,但在不同地点长度比是不同,即不同地点上的变形椭圆大小不同。等积投影:定义为即在投影平面上任意一块面积与椭球面上相应的面积相等,即面积变形等于零。等距投影:在任意投影上,长度、面积和角度都有变形,它既不等角又不等积。但是有一种比较常见的等距投影,定义为沿某一特定方向的距离,投影前后保持不变。在这种投影图上并不是不存在长度变形,它只是在特定方向上没有长度变形。等距投影的面积变形小于等角投影,角度变形小于等积投影。地理信息系统geographicalinformationsystem中南大学地信0802欧阳芳列表对比为:名称特点适用范围等角投影无角度变形航海、空图、洋流图、风向图、气象图及军用地图等积投影无面积变形经济图,行政区图和人口图等距投影(属于任意投影的特殊情况)特定方向上无长度变形沿某一特定方向量测距离的地图、教学地图和交通地图2.常用的几何投影:方位投影:以平面作为投影面,使平面与球面相切或相割,将球面上的经纬线投影到平面上而成。其中球心投影常用于航空及航海图,外心投影常用于空间透视投影。圆柱投影:以圆柱面作为投影面,使圆柱面与球面相切或相割,将球面上的经纬线投影到圆柱面上,然后将圆柱面展为平面而成。圆锥投影:以圆锥面作为投影面,使圆锥面与球面相切或相割,将球面上的地理信息系统geographicalinformationsystem其变形性质在微分圆上的表示为中南大学地信0802欧阳芳经纬线投影到圆锥面上,然后将圆锥面展为平面而成。圆锥投影,圆柱投影,以及方位投影的情况分别用图形表示为:方位投影,圆锥投影,圆柱投影的异同分析(此表格中不加特别说明则默认为正轴投影):名称方位投影圆柱投影圆锥投影投影面平面圆柱面圆锥面纬线投影特点同心圆平行直线同心圆圆弧经线投影特点同心圆的半径与纬线投影成的垂直于同心圆弧地理信息系统geographicalinformationsystem中南大学地信0802欧阳芳平行直线垂直的平行直线且相交于一点的直线束投影变形分析经线间的夹角与实地经度差相等,其等变形线为圆形其变形只与纬度有关,与经差无关,同纬度上各点的变形相同其变形只与纬度有关,与经差无关,同纬度上各点的变形相同适用范围具有圆形轮廓的区域和两极地区低纬度沿纬线伸展的区域中纬度处沿纬线伸展的区域习惯特殊投影方式及用途1.正轴等角方位投影:极球面2.等积方位投影:小比例尺地图,东西半球图3.正轴等距方位投影:南北极图4.横轴等距方位投影:东西半球图5.斜轴等距方位投影:航空中心站,地震观测中心,气象站等需满足到中心距离相等的勘测中心。1.等角圆柱投影(墨卡托投影):世界时区图,大圆航线(航空及航海图)1.正轴等面积圆锥投影:行政区域图,人口地图,社会经济等用面积表达一定含义的地图2.等角圆锥投影(兰伯特投影):中纬度地区3.正轴割等角圆锥投影:中纬度地区的中小比例尺地图兰伯特投影,通用横轴墨卡托(Mercator)投影,高斯克吕格投影的对比分析:名称兰伯特投影通用横轴墨卡托(Mercator)投影高斯克吕格投影类型等角圆锥投影横轴等角割圆柱投影等角横切椭圆柱投影投影特点纬线投影为同心如图示:如图示:地理信息系统geographicalinformationsystem中南大学地信0802欧阳芳圆圆弧,经线垂直于同心圆弧且相交于一点的直线束变形分析其变形只与纬度有关,与经差无关,同纬度上各点的变形相同,且无角度变形在赤道上离中央经线大约180km位置的两条割线上没有任何变形,距这两条割线越远变形愈大无角度变形,中央经线上没有变形,同一条纬线上离中央经线越远变形越大,同一条经线上纬度越低变形越大地理信息系统geographicalinformation...