材料力学第4章第5章VIP免费

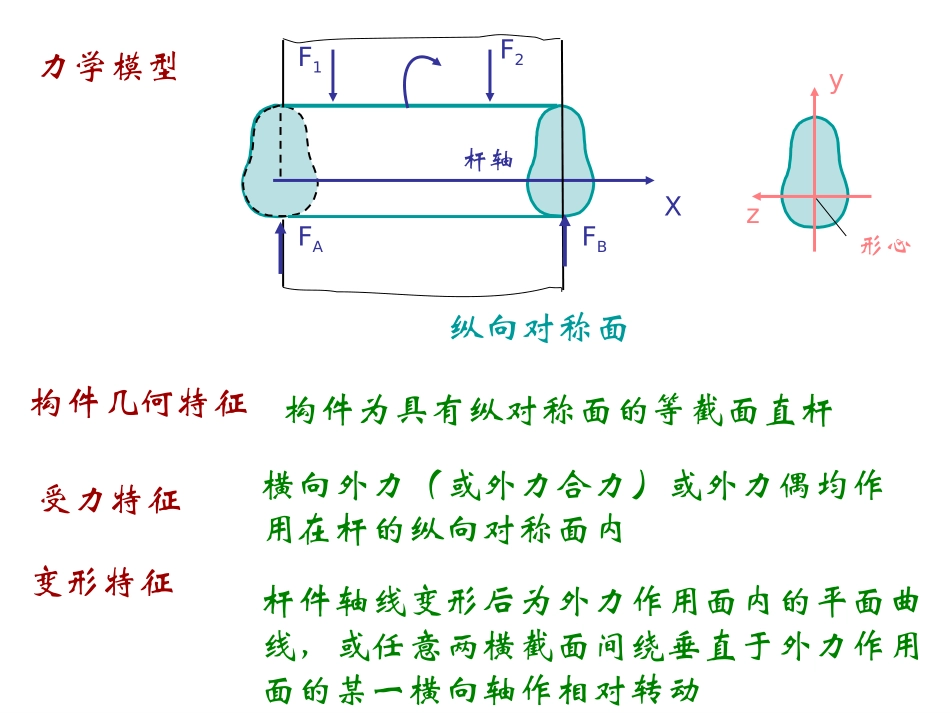
第四章弯曲内力§1弯曲的概念和实例力学模型X杆轴纵向对称面F1F2FAFB构件几何特征构件为具有纵对称面的等截面直杆yz形心受力特征横向外力（或外力合力）或外力偶均作用在杆的纵向对称面内变形特征杆件轴线变形后为外力作用面内的平面曲线，或任意两横截面间绕垂直于外力作用面的某一横向轴作相对转动对称弯曲构件的几何形状、材料性能和外力作用均对称于杆件的纵对称面X杆轴纵向对称面F1F2FAFB平面弯曲梁变形后的轴线所在平面与外力所在平面相重合qFeMAyFByFxBAy对称面向纵对称弯曲必定是平面弯曲，而平面弯曲不一定是对称弯曲。非对称弯曲构件不具有纵对称面，或虽有纵对称面但外力不作用在纵对称面时的弯曲变形梁：以弯曲变形为主的杆件静定梁支座反力可以由静力平衡方程求解的梁超静定梁支座反力仅由静力平衡方程不能求解的梁墙梁楼板ql一、支座的几种基本形式悬臂梁3（2）简支梁3（2）外伸梁3（2）固定梁6（4）连续梁4（3）半固定梁4（3）§2受弯杆件的简化均匀分布荷载线性(非均匀)分布荷载分布荷载Me集中力偶集中力二、载荷的简化q2ll§3剪力和弯矩左端是固定铰支约束，右端是可动较支约束，为简支梁若约束反力、已求得，用截面法可以求梁任意横截面I—I上的内力：剪力、弯矩的正负号剪力（shearingforce）弯矩（bendingmoment）该截面一侧横向力的代数和该截面一侧横向力矩的代数和使微段梁有顺时针转动趋势的剪力为正，反之为负；使微段梁产生向下凸变形的弯矩为正，反之为负。符号规定：符号规定：Fs＞0Fs＜0M＞0M＜0例4-1外伸梁受力与支承情况如图7所示，求1-1、2-2两截面的剪力与弯矩。解：1）求约束反力2）求1-1截面上的剪力、弯矩3）求2-2截面上的剪力、弯矩lFl2FlACDB例4-2试确定截面C及截面D上的剪力和弯矩CsFlACAFAMAFAMFFCsCMFlMCFl2FlCDBCsFCMFFCs02FlFlMCFlMCBFDDsFDMFFDs0DMkN29030kN1502335.460yBBAAABFqFFFFFqFFMmkN26)5.12(2kN7A1A1SFFMFFFmkN3025.15.15.1kN115.1B2B2SqFMFqF例4-3求下图所示简支梁1-1与2-2截面的剪力和弯矩。2112m21.5mq=12kN/m3m1.5m1.5mF=8kNABFAFB解：1、求支反力2、计算1-1截面的内力3、计算2-2截面的内力F=8kNFAS1F1MFBq=12kN/mS2F2M例4-4外伸梁受力与支承情况如图7所示，求1-1、2-2两截面的剪力与弯矩。解：1）求约束反力2）求1-1截面上的剪力、弯矩3）求2-2截面上的剪力、弯矩向上的外力引起正剪力，向下的外力引起负剪力；截开后取左边为示力对象：向上的外力引起正弯矩，向下的外力引起负弯矩；顺时针引起正弯矩，逆时针引起负弯矩。向上的外力引起负剪力，向下的外力引起正剪力；截开后取右边为示力对象：向上的外力引起正弯矩，向下的外力引起负弯矩；顺时针引起负弯矩，逆时针引起正弯矩。lFaABFAFBFAFsxASFFMxFMA§4剪力方程和弯矩方程剪力图和弯矩图qlABFAFBxqxqlFS2222qxxqlM2ql2ql82ql例4-5图示悬臂梁AB,自由端受力F的作用,试作剪力图和弯矩图.lABFXFxFSLx0FxxMLx0FFLkNkNm例4-6如图所示简支梁，受集中力F作用，试写出梁的剪力方程和弯矩方程，并作剪力图与弯矩图。解：1）求约束反力并验算2）分段列剪力与弯矩方程AC段：BC段：如图所示简支梁，受集中力F作用，试写出梁的剪力方程和弯矩方程，并作剪力图与弯矩图。解：1）求约束反力并验算2）分段列剪力与弯矩方程AC段：BC段：3）作剪力图与弯矩图例4-7如图所示外伸梁，F、a已知，试作其、Mz图。解：1）求约束反力并验算2)分段列内力方程CA段：AD段：DB段：3）画出梁的剪力图和弯矩图例4-8如图所示简支梁承受均布载荷作用，载荷集度为q，梁的长度为l，试作梁的、Mz图。解：1）求约束反力并验算2)列内力方程3）画剪力图和弯矩图x=l/2，弯矩有极大值Mzmax=ql2/8§5载荷、剪力与弯矩间的关系内力突变规律qdxMdFdxdMqdxdFSs220dxdFsCFS剪力图是水平直线.CdxdM弯矩图是斜直线.0dxdMCM弯矩图是水平直线.qdxdFs剪力图是斜直线.弯矩图是二次抛物线.dxxqdFxxFFSSS2121211...