第9章静电场中的导体VIP免费

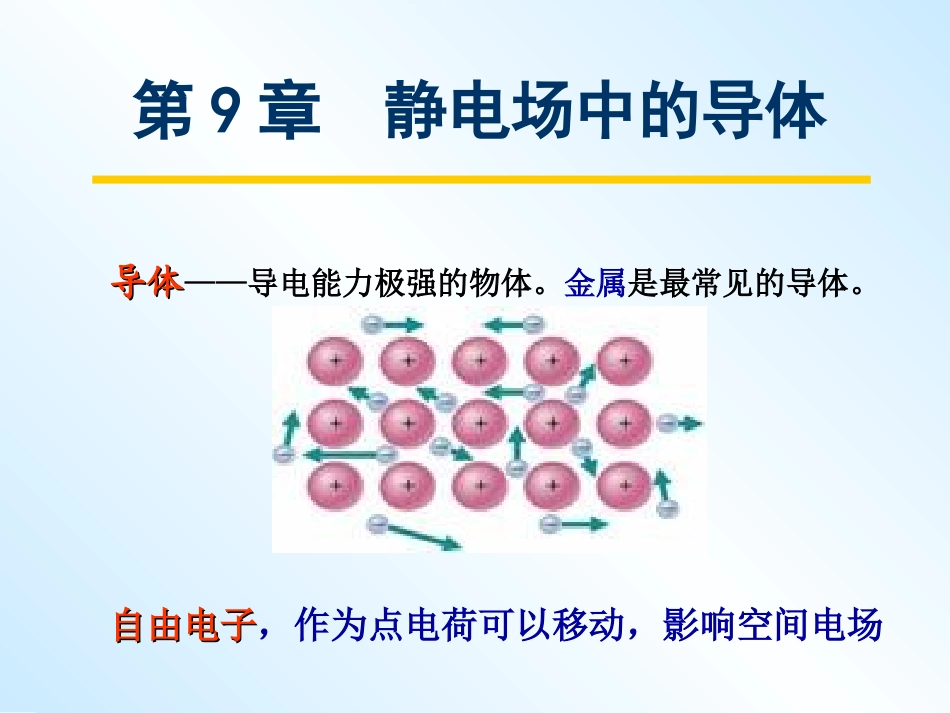
第第99章章静电场中的导体静电场中的导体ConductorsinElectrostaticFieldConductorsinElectrostaticField本章主要内容§9-1§9-1导体的静电平衡条件§9-2§9-2静电平衡导体上的电荷分布§9-3§9-3有导体时静电场分布的计算§9-4§9-4静电屏蔽§9-1§9-1导体的静电平衡条件§9-2§9-2静电平衡导体上的电荷分布§9-3§9-3有导体时静电场分布的计算§9-4§9-4静电屏蔽第9章静电场中的导体导体导体——导电能力极强的物体。金属是最常见的导体。自由电子自由电子，作为点电荷可以移动，影响空间电场§9-1§9-1导体的静电平衡条件导体的静电平衡条件ElectrostaticEquilibriumConditionElectrostaticEquilibriumConditionofaConductorofaConductor理解并应用“同性相斥，异性相吸”能够想象出“静电平衡”就是动态地建立起来的能够想象出“静电平衡”就是动态地建立起来的地球上有一片带电的云地球上有一片带电的云++++++++++++++++++++++++++++地球地球++++++++++++++++++++++++++++------------------------宏观上：带电体总是吸引不带电的物体过程：带电体的电场破坏不带电物体的电中性宏观上：带电体总是吸引不带电的物体过程：带电体的电场破坏不带电物体的电中性在外加电场的作用下，导体上宏观电荷产生运动而使宏观电荷重新分布（对均匀导体来说表现在表面），这种现象称为静静电感应电感应；由静电感应而产生的宏观电荷称为感应电荷。electrostaticinduction+++++-----eFeF静电平衡静电平衡——导体内部和表面的宏观电荷无定向移动。静电平衡的条件条件是：导体内部场强处处为零。这一条件与导体形状无关，且是充分必要的。0intE静电平衡条件的推论推论：（1）导体是一个等势体，导体表面是等势面；（2）导体表面紧邻处的场强与导体表面正交。证明（2）：设R和S各为导体表面紧邻处的两点，由于导体表面是等势面，则0lE邻lE邻PQRS邻El证明（1）：在导体内部和表面任取P，Q和R各点，0,0intintintRPQPrdErdEERQP即§9-2§9-2静电平衡导体静电平衡导体上的电荷分布上的电荷分布ChargeDistributiononaConductorChargeDistributiononaConductorunderElectrostaticEquilibriumunderElectrostaticEquilibrium（1）静电平衡导体上的电荷分布证明：设导体内A点有点电荷q时，取足够小的球形高斯面S包围q，E4r2=q/0，E=q/(40r2)，即Eint0，与静电平衡条件矛盾。实心导体：内部无净电荷，电荷只能分布在导体表面。S.q带空腔导体：如果空腔内无带电体，电荷只分布在外表面；如果空腔内有带电体，空强内壁的净电荷总是与空强内带电体的电量等异号，其余电荷均分布在外表面。SSQP证明：（1）无论空腔内有无导体，取导体内部的高斯面S包围整个空腔，则有，q=0；（2）如果空腔内无电荷，设在内壁P点有正电荷、Q点有负电荷，则，但，矛盾。00intSSqSdE内0intLQPrdE-..+PQL（2）静电平衡导体表面电荷与场强的关系处于静电平衡的导体表面某点的面电荷密度，正比于该点紧邻处的场强大小；处于静电平衡的孤立导体，其表面某处的面电荷密度，正比于该处表面的曲率。SE证明：取底面积为S的柱状高斯面，0SSESdE0E证明略nE尖端放电曲率0E金属导体处于静电平衡时，有应用：打火装置，避雷针等强电场中的空气分子被电离，形成导电气体，导致放电产生。§9-3§9-3有导体时静电场有导体时静电场分布的计算分布的计算ComputationofDistributionofanElectro-ComputationofDistributionofanElectro-staticFieldwhenExistingConductor(s)staticFieldwhenExistingConductor(s)例如：一块孤立的带电导体平板，面积为S，电量为q，求紧邻导体板处的场强。在涉及导体的静电场问题中，静电平衡导体表面电荷和其外部空间的电场分布是唯一的、确定的。求解这种问题需要考虑以下规律：静电场的基本性质（如场强叠加原理，Gauss定理等）电荷守恒定律；静电平衡条件。12两侧的面电荷密度相等（曲率均为零...