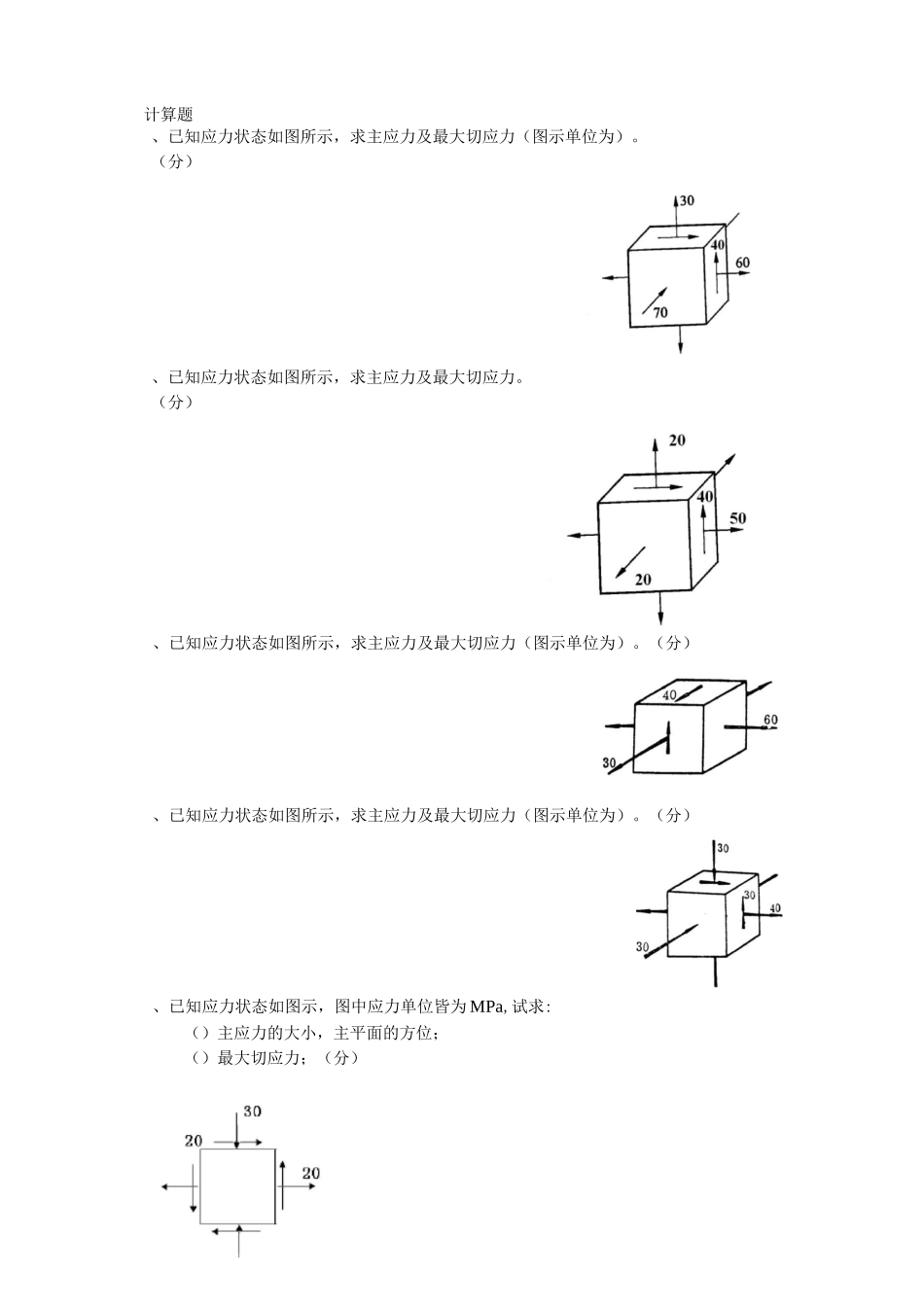
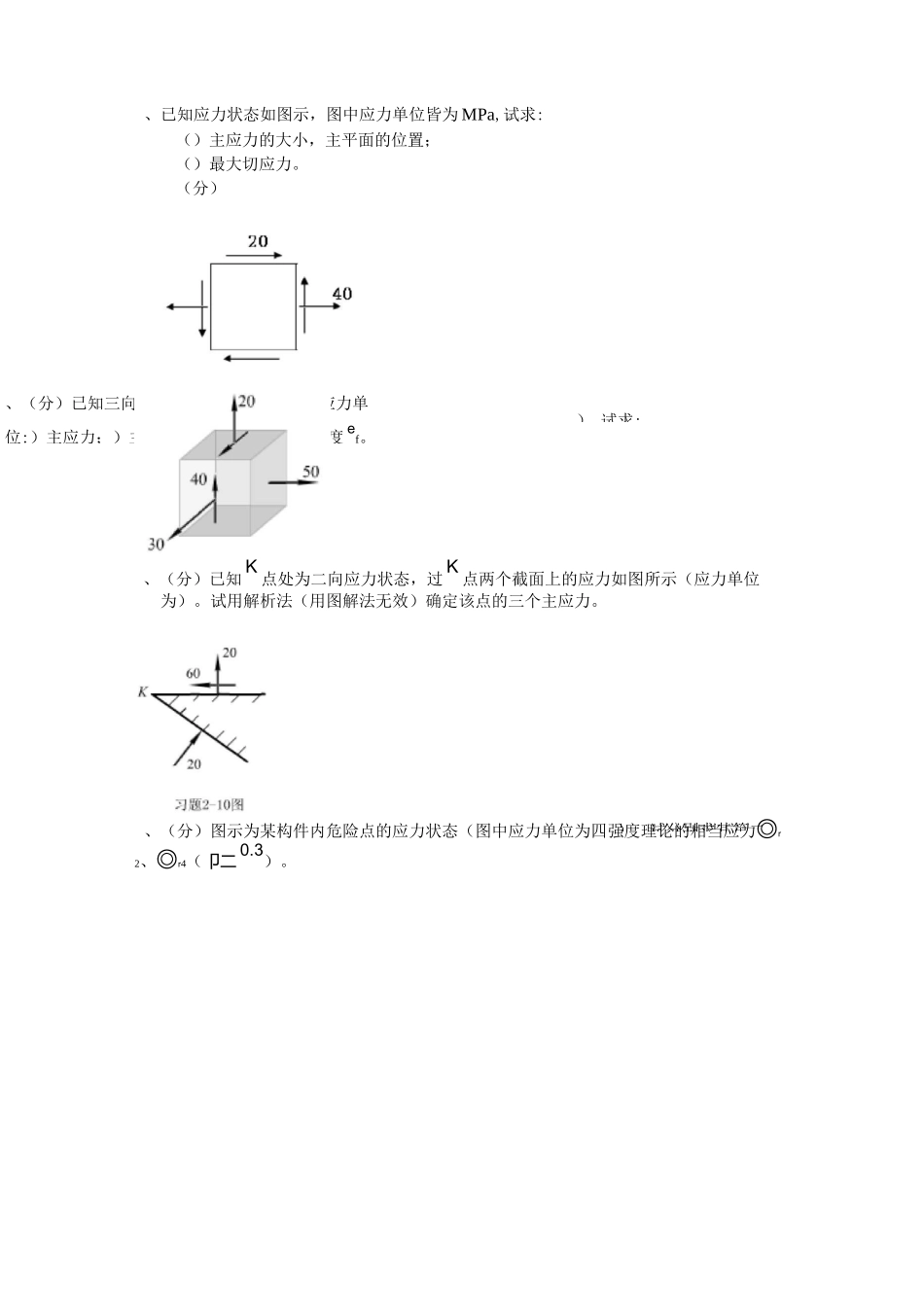
计算题、已知应力状态如图所示,求主应力及最大切应力(图示单位为)。(分)、已知应力状态如图所示,求主应力及最大切应力。(分)、已知应力状态如图所示,求主应力及最大切应力(图示单位为)。(分)、已知应力状态如图所示,求主应力及最大切应力(图示单位为)。(分)、已知应力状态如图示,图中应力单位皆为MPa,试求:()主应力的大小,主平面的方位;()最大切应力;(分)、(分)已知三向应力状态如图所示(图中应力单位:)主应力;)主切应力;)形变应变能密度ef。),试求:),试分别求其第二、、已知应力状态如图示,图中应力单位皆为MPa,试求:()主应力的大小,主平面的位置;()最大切应力。(分)、(分)已知K点处为二向应力状态,过K点两个截面上的应力如图所示(应力单位为)。试用解析法(用图解法无效)确定该点的三个主应力。、(分)图示为某构件内危险点的应力状态(图中应力单位为四强度理论的相当应力◎r2、◎r4(卩二0.3)。、(分)图示为某构件内危险点的应力状态(图中应力单位为第四强度理论的相当应力r2、r4(卩二0.3)。),试分别求其第、(分)矩形截面细长悬臂梁如图所示。试求、、三点的应力,并用单元体分别表示这三点的应力状态。、(分)已知构件内某点处的应力状态为两种应力状态的叠加结果,试求叠加后该点该平面内的()主应力与主应变;()主切应力;e()该点的形变应变能密度f。(已知材料的弹性模量E=200GPa,横向变形系数v=0.3)、图示板件,微体处于纯剪切应力状态,试计算沿对角线AC与BD方位的正应力,以及所对应力正应变£与£,沿板厚方向的正应变*。材料的弹性常数E与卩均为已450-450z知。、图示直径为d的圆截面轴,其两端承受扭力矩M作用。设由实验测得轴表面与轴线成9二45。方向的正变应£,试求该扭力偶矩M之值。材料的弹性常数E与卩均为已ab知。二、图示微体处于平面应力状态,应力单位为MPa,试求:指定斜截面上的正应力与切应力;主应力所在主平面的方位;最大切应力。、某点的应力状态如图所示。已知o和最大剪应力;、该点属于何种应力状试求:、该点的主应、已知应力状态如图所示应力单位MPa,求:应力;主应力及所在截面的方位。指定截面上的正应力与、图示矩形截面杆,承受轴向载荷F作用,试计算线段AB的正应变。设横截面的高度h、宽度b以及材料的弹性常数E与卩均为已知。、、已知应力状态如图示,图中应力单位皆为MPa,试求:()主应力的大小,主平面的方位;()最大切应力;(分)/T—/、已知应力状态如图示,图中应力单位皆为MPa,试求:()主应力的大小,主平面的位置;()最大切应力。()在单元体上绘出主平面位置及主应力方向;、图示微体处于平面应力状态,应力单位为MPa,试求:指定斜截面上的正应力与切应力;主应力所在主平面的方位;最大切应力。SO■/()、知应力状态如图所示应力单位MPa,求:指定截面上的正应力与切应力;主应力及所在截面的方位。.某点的应力状态如图所示,试求:该点的主应力大小与方向;该点的最大切应力;在单元体上画出主应力的方向(图中应力单位:MPa)。、(分)已知三向应力状态如图所示(图中应力单位:),试求:e)主应力;)主切应力;)形变应变能密度f。解:()平行于木纹方向切应力—4—(-16)T=——sin(2x(—15。))+0-cos(2x(—15。))=0.6x'y'2垂直于木纹方向正应力2MP0.5MPa习题5-2—木制构件中的微元受力如图所示,其中所示的角度为木纹方向与铅垂方向的夹角。试求:bx,—4+(—1.6)+-4-(-L6)cos(2x(—15。))+0=—3.842()切应力T=—1.25cos(2x(—15°))=—1.08x,y,正应力b=—(—1.25)sin(2x(—15°))=—0.625x,—层合板构件中微元受力如图所示,各层板之间用胶粘接,接缝方向如图中所示。若已知胶层切应力不得超过。试分析是否满足这一要求。解:T=—2—(—1)sin(2x(—60°))+0.5-cos(2x(—60°))=—1.55x,y,2IT1=1.55MPa>1,不满足。x,y,—结构中某点处的应力状态为两种应力状态的叠加结果。试求叠加后所得应力状态的主应力、面内最大切应习力题和5-2该图点处的最大切应力。bx,bx,