浅析竞赛中一类数学期望问题的解决方法VIP免费

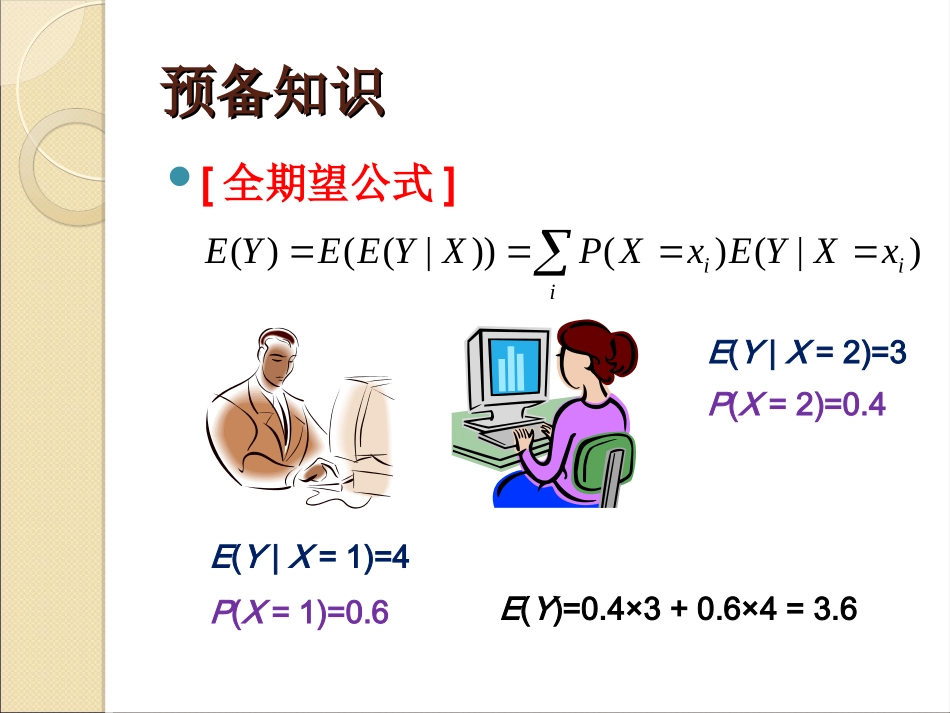
浅析竞赛中一类数学期望问题浅析竞赛中一类数学期望问题的解决方法的解决方法福建省福州第八中学汤可因预备知识预备知识[什么是数学期望]如果X是一个离散的随机变量，输出值为x1,x2,...，和输出值相应的概率为p1,p2,...（概率和为1）,那么期望值iiixpXE)(预备知识预备知识[全期望公式]iiixXYExXPXYEEYE)|()())|(()(E(Y|X=1)=4E(Y|X=2)=3P(X=2)=0.4P(X=1)=0.6E(Y)=0.4×3+0.6×4=3.6引言引言一、利用递推或动态规划解决二、建立线性方程组解决模型例题：FirstKnight例题：Mario引入模型引入模型给出一张有向图G=(V,E)。顶点i的权值为Wi。给出Pu,v表示顶点u经过边(u,v)到顶点v的概率。若某点i发出边概率和为Pi，那么在顶点i时有1－Pi的概率停止行动。定义路径权为这条路径上所有点权之和。问从一个顶点s开始，在每次按照指定的概率走的前提下，到某一顶点停止行动时所走的路径权的期望值。引入模型引入模型例如这张有向图，s=1。W1=W2=W3=1，W4=0。可以看到有两条路径。两条路径权分别为3和2，而走这两条路径的概率均为0.5。所以得到的期望为2.5=0.5×3+0.5×2。123410.50.51引入模型引入模型对于这种不存在环的有向图。设Fi表示从顶点i出发的路径权期望。可以分成两类情况。从顶点i出发经过相邻顶点k的路径权期望为Fk+Wi，概率Pi,k。停止行动路径权Wi。123410.50.51引入模型引入模型可以得到如下的递推式并按照拓扑序来递推但若将这张有向图稍作修改123410.50.51EkiijkkijiWFPF),(1,,,引入模型引入模型可以得到如下的递推式并按照拓扑序来递推但若将这张有向图稍作修改图存在环。EkiijkkijiWFPF),(1,,,123410.50.51引入模型引入模型所以对于一般的有向图，可以设Fi,j为从顶点i出发，经过j步所走路径的路径权期望。那么有：当j>0时iiWF0,EkiijkkijiWFPF),(1,,,123410.50.51引入模型引入模型所以对于一般的情况，可以设Fi,j为从顶点i出发，经过j步所走路径的路径权期望。那么有：当j>0时iiWF0,EkiijkkijiWFPF),(1,,,若Fi,j当j→∞时收敛，设收敛于Fi那么答案即为Fs。123410.50.51引入模型引入模型若Fi,j当j→∞时收敛，设收敛于Fi那么答案即为Fs。可以利用迭代求出满足精度要求的解，但是时间复杂度无法接受。EkiijkkijiWFPF),(1,,,123410.50.51引入模型引入模型方程形式：对于右图可以得到如下方程组EkiijkkijiWFPF),(1,,,015.05.01144133221FFFFFFFF123410.50.51引入模型引入模型高斯消元EkiijkkijiWFPF),(1,,,1-100101-101-0.501-0.5100010123410.50.51引入模型引入模型方程组中只含有与s相关的点。方程组没有唯一解的情况。可以调整消元顺序让所要求的Fs放在最后，这样就可以不用回代。若权在边上而不在点上的话，设边(u,v)的权值为Wu,v，那么同理方程即为EjijijjiiWFPF),(,,)(例题：例题：FirstKnightFirstKnight题目来源：SWERC08一个m×n的棋盘，左上至右下编号为(1,1)至(m,n)，并给定每个格子到周围四个格子的概率。一个骑士从(1,1)开始，按照给定概率走，问到达(m,n)的期望步数。题目保证从任一格开始到(m,n)的概率均为1。)(,kjiP[问题描述]例题：例题：FirstKnightFirstKnight列出方程直接求解？Ei,j表示从(i,j)出发的步数期望。11,)4(,,1)3(,1,)2(,,1)1(,,jijijijijijijijijiEPEPEPEPEm,n≤40Accept?时间复杂度O(m3n3)Timelimitexceeded进行优化！进行优化！[分析]例题：例题：FirstKnightFirstKnight方程未知量第i行第j列的格子表示了方程：11,)4(,,1)3(,1,)2(,,1)1(,,jijijijijijijijijiEPEPEPEPE[优化]例题：例题：FirstKnightFirstKnight方程未知量第i行第j列的格子表示了未知量：jiE,[优化]例题：例题：FirstKnightFirstKnight同样为了避免回代，可以以逆序也就是Em,n到E1,1的顺序进行消元。123……方程未知量[优化]例题：例题：FirstKnightFirstKnight对于方程而言，若当前...