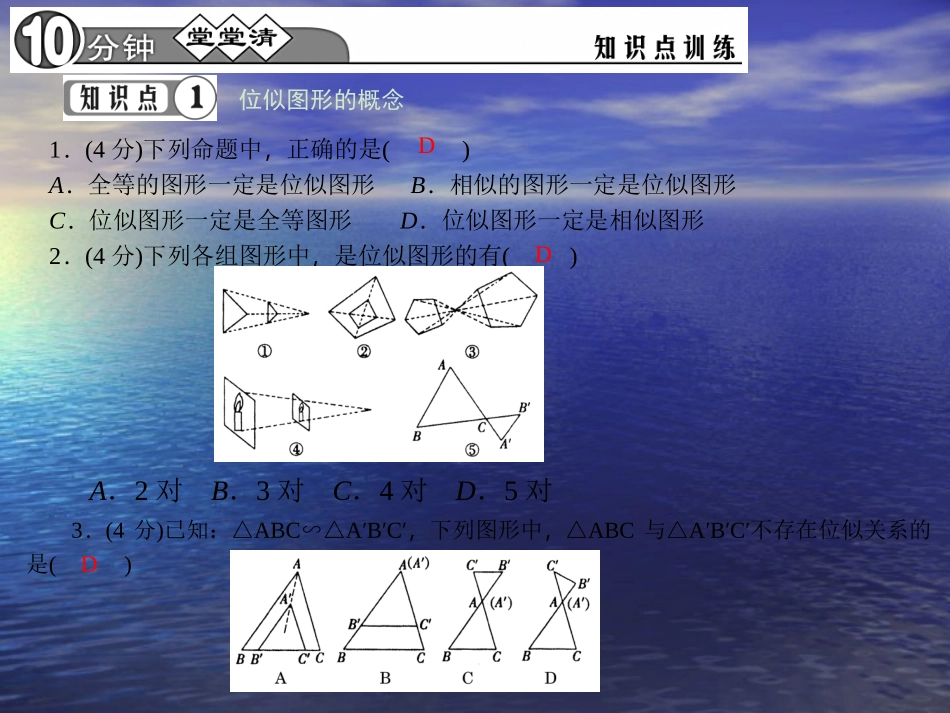
第二十七章图形的相似27.3位似第1课时位似的概念及性质1.如果两个多边形不仅是相似图形,而且对应顶点的连线__,对应边互相平行那么这样的两个图形叫做位似图形,这个点叫做__.2.位似图形上任意一对对应点到位似中心的距离之比等于__,位似图形的对应边分别__或_.相交于一点位似中心相似比平行在同一条直线上位似图形的概念1.(4分)下列命题中,正确的是()A.全等的图形一定是位似图形B.相似的图形一定是位似图形C.位似图形一定是全等图形D.位似图形一定是相似图形2.(4分)下列各组图形中,是位似图形的有()A.2对B.3对C.4对D.5对3.(4分)已知:△ABC∽△A′B′C′,下列图形中,△ABC与△A′B′C′不存在位似关系的是()DDD位似图形的性质4.(4分)如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,已知OA=10cm,OA′=20cm,则五边形ABCDE的周长与五边形A′B′C′D′E′的周长的比值是__.5.(4分)如图,△ABC与△A′B′C′是位似图形,点O是位似中心,若OA=2AA′,S△ABC=8,则S△A′B′C′=__.6.(4分)如图,四边形ABCD与四边形AEFG是位似图形,且AC∶AF=2∶3,则下列结论不正确的是()A.四边形ABCD与四边形AEFG是相似图形B.AD与AE的比是2∶3C.四边形ABCD与四边形AEFG的周长比是2∶3D.四边形ABCD与四边形AEFG的面积比是4∶91218B7.(8分)如图,已知△DEO与△ABO是位似图形,△OEF与△OBC是位似图形,试说明:OD·OC=OF·OA.解:由DEO△与ABO△位似得到ODOA=OEOB;由OEF△与OBC△位似可得OEOB=OFOC,∴ODOA=OFOC,即OD·OC=OF·OA位似图形的画法8.(8分)如图,以O为位似中心,将四边形ABCD缩小为原来的一半.解:图略一、选择题(每小题6分,共18分)9.“标准对数视力表”对我们来说并不陌生,如图是视力表的一部分,其中最上面较大“E”与下面四个较小“E”中的哪一个是位似图形()A.左上B.左下C.右上D.右下10.图中两个四边形是位似图形,它们的位似中心是()A.点MB.点NC.点OD.点P11.如图,下列由位似变换得到的图形中,面积比是1∶9的是()A.OA=1.2OA′B.OA=AA′C.OA=2AA′D.OA=12AA′BDD二、填空题(每小题6分,共12分)12.如图所示,三角尺在灯泡O的照射下在墙上形成影子,现测得OA=20cm,OA′=50cm,这个三角尺的周长与它的墙上形成的影子的周长比是__.13.如图,△ABC与△A1B1C1是位似图形,点O是它们的位似中心,位似比是1∶2,已知△ABC的面积为3,那么△A1B1C1的面积是__.三、解答题(共30分)14.(8分)如图,△ABC与△A′B′C′是位似图形,且位似比是1∶2,若AB=2cm,则A′B′=_4_cm,并在图中画出位似中心O.解:图略2∶51215.(10分)如图,矩形ABCD与矩形A′B′C′D′是位似图形,A是位似中心,已知矩形ABCD的周长为24,BB′=4,DD′=2,求AB和AD的长.解:∵矩形ABCD的周长为24,∴AB+AD=12,设AB=x,则AD=12-x,∴AB′=x+4,AD′=14-x,∵矩形ABCD与矩形A′B′C′D′是位似图形,∴矩形ABCD∽矩形A′B′C′D′,∴ABA′B′=ADA′D′,即xx+4=12-x14-x,解得x=8,∴AB=8,AD=12-x=4.16.(12分)如图,在6×8网格图中,每个小正方形边长均为1,点O和△ABC的顶点均在小正方形的顶点上.(1)以O为位似中心,在网格图中作△A′B′C′和△ABC位似,且相似比为1∶2;(2)连接(1)中的AA′,求四边形AA′C′C的周长.(结果保留根号)解:(1)图略(2)AA′=CC′=2,在Rt△OA′C′中,OA′=OC′=2,得A′C′=22,于是AC=42,∴四边形AA′C′C的周长=4+62