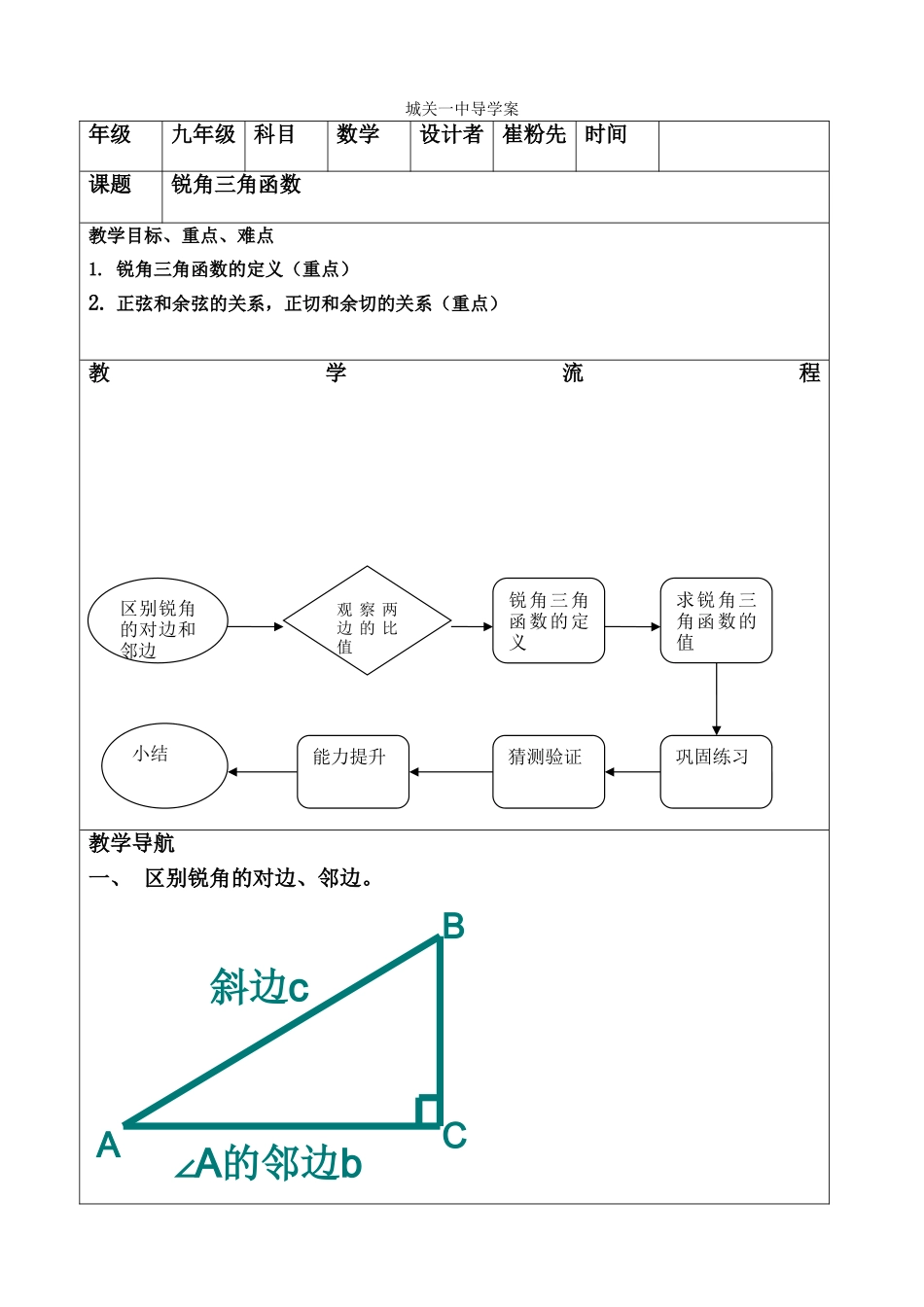
城关一中导学案年级九年级科目数学设计者崔粉先时间课题锐角三角函数教学目标、重点、难点1.锐角三角函数的定义(重点)2.正弦和余弦的关系,正切和余切的关系(重点)教学流程教学导航一、区别锐角的对边、邻边。区别锐角的对边和邻边小结观察两边的比值锐角三角函数的定义求锐角三角函数的值巩固练习猜测验证能力提升BAC∠A的邻边b斜边c二、让生观察得出:在Rt△ABC中对于锐角A的每一个确定的值其对边与邻边的比值也固定不变。并猜测对于锐角A的每一个确定的值其对边与斜边的比、邻边与斜边的比、对边与邻边的比、邻边与对边的比是唯一确定的吗?三、锐角三角函数定义:1、sinA=∠A的对边/斜边2.cosA=∠A的邻边/斜边3、tanA=∠A的对边/∠A邻边4、cotA=∠A的邻边/∠A对边5、sinA,cosA,tanA,cotA分别叫做∠A的正弦余弦正切余切,统称为锐角∠A的三角函数。AC1C2C3B3B1B2四、巩固练习:1、下图中∠ACB=90°,(1)指出∠A的对边、邻边。2、上题中如果CD=5,AC=10,则sinA=求出如图所示的Rt△ABC中∠A的四个三角函数值.五、猜一猜做一做1.设Rt△ABC中∠ACB=90°,∠A∠B、∠C的对边分别a、b、c根据下列条件求∠B的四个三角函数值(1)a=3b=4(2)a=5c=132.tanA•cotA=六、能力提升:(1)在Rt△ABC中∠ACB=90°,BC:AC=3:4cosA=(2)()·cot20º=1(4)把Rt△ABC的各边都扩大5倍得Rt△A1B1C1则锐角A,A1的余弦值关系是()AcosA=cosA1B3cosA=cosA1CcosA=3cosA1D不能确定七、谈谈本节课的收获。CBA68ACBCD