分式方程(第1课时)VIP免费

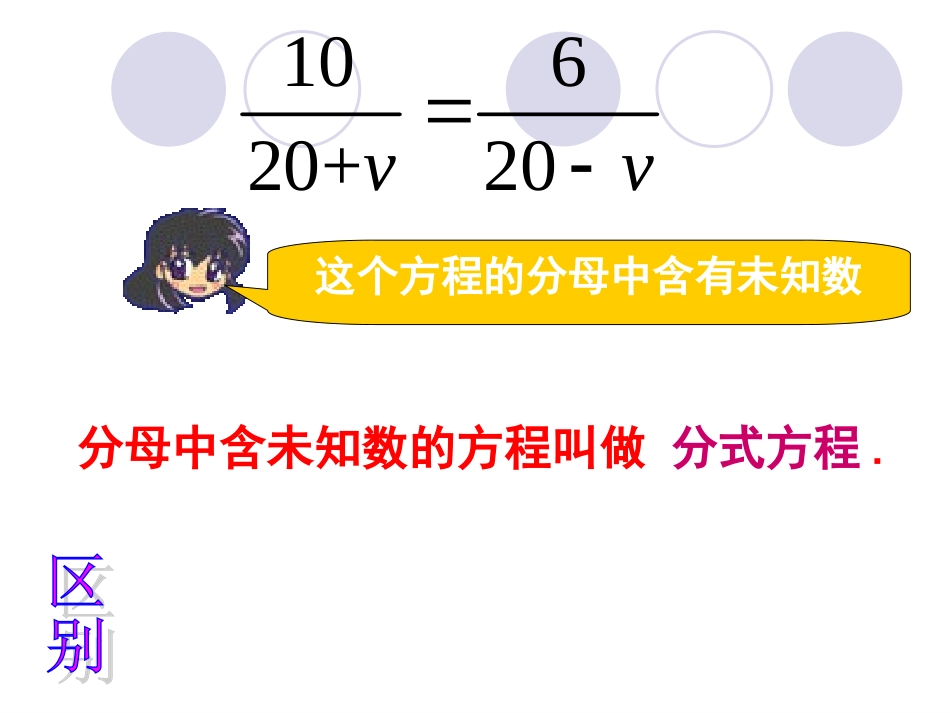
1.什么叫做一元一次方程?2.下列方程哪些是一元一次方程?回顾与思考回顾与思考3.什么叫做分式方程?分母中不含未知数的方程叫做整式方程.35x3)1(5y2x)2(5xx)3(21312)4(xx这个方程的分母中含有未知数【分式方程的定义】分母中含未知数的方程叫做分式方程.整式方程的未知数不在分母中分式方程的分母中含有未知数10620+20vv（否）（是）（是）（是）是分式方程34443)2(xx是分式方程5232)1(x是分式方程1)3(2xx是分式方程1111)4(yx2131xxx437xy下列方程中，哪些是分式方程？哪些整式方程.整式方程分式方程1312xx解方程回顾与思考回顾与思考6)1(23xx6223xx8x4、化系数为1.1、去分母2、去括号.3、移项.合并同类项步骤解:如何求分式方程的解呢?去掉分母，化为整式方程。如何去掉分母，化为整式方程还保持等式成立?730100xx解方程730100xx解方程两边同乘以x(x-7),约去分母,得100(x-7)=30x解这个整式方程,得X=10检验:把x=10代入x(x-7),得10×(10-7)≠0所以,x=10是原方程的解.22162242xxxxx(2(2))解：方程两边同乘以),2)(2(xx,)2(16)2(22xx得，,44164422xxxx.2x检验：把x=2代入x2-4，得x2-4=0。∴x=2是增根，从而原方程无解。.注意：分注意：分式方程的式方程的求根过程求根过程不一定是不一定是同解变形，同解变形，所以分式所以分式方程一定方程一定要验根！要验根！解分式方程的一般步骤:1.去分母。化分式方程为整式方程.即把分式方程两边同乘以最简公分母.2.解这个整式方程.3.检验.把整式方程的解(根)代入最简公分母,若结果为零则是增根,必须舍去,若结果不为0,则是原方程的根.4.写结论)2)(1(311:xxxx解方程类似的在将分式方程变形为整式方程时，方程两边同乘以一个含未知数的整式，并约去了分母，有时可能产生不适合原分式方程的解（或根），这种根通常称为增根.因此，在解分式方程时必须进行检验.那么，可能产生“增根”的原因在哪里呢？探究分式方程的增根原因探究分式方程的增根原因探究分式方程的增根原因探究分式方程的增根原因对于原分式方程的解来说，必须要求使方程中各分式的分母的值均不为零，但变形后得到的整式方程则没有这个要求.如果所得整式方程的某个根，使原分式方程中至少有一个分式的分母的值为零，也就是说使变形时所乘的整式（各分式的最简公分母）的值为零，它就不适合原方程，即是原分式方程的增根.解分式方程的一般步骤1、去分母，2、解整式方程.3、验根4、写结论.解分式方程的思路是：分式方程整式方程去分母验根等号两边都乘以最简公分母解方程:（1）（2）（3）（4）3221xx14122xx01522xxxx13321xxxx22231xxxxxx23123221122xxx通过例题的讲解和练习的操作,你能总结出解分式方程的一般步骤吗?【小结】解分式方程的一般步骤:分式方程整式方程a是分式方程的解X=aa不是分式方程的解去分母解整式方程检验目标最简公分母不为０最简公分母为０1.若方程中的分母是多项式,须先分解因式.再确定最简公分母.2.若方程中的含有整数项,去分母时不要漏乘.课堂练习6x+m3例3:当m=_____时,----+-----=-------有增根.xx-1x(x-1)解:在方程两边都乘以x(x-1)得3(x-1)+6x=x+m所以8x-m-3=0.因为方程的增根是x=0或x=1所以m=-3或m=5.1.若方程------=-1的解是负数,求a的取值范围.2x+ax-22.a为何值时,关于x的方程------=------的解等于0.x+1x-22a-3a+53.a为何值时关于x的方程53221aaxx的解是零.4.011||xx的根是______5.方程1112xxx的增根是（）,根是（）。6.关于x的方程8778xkxx有增根,则k=_____.