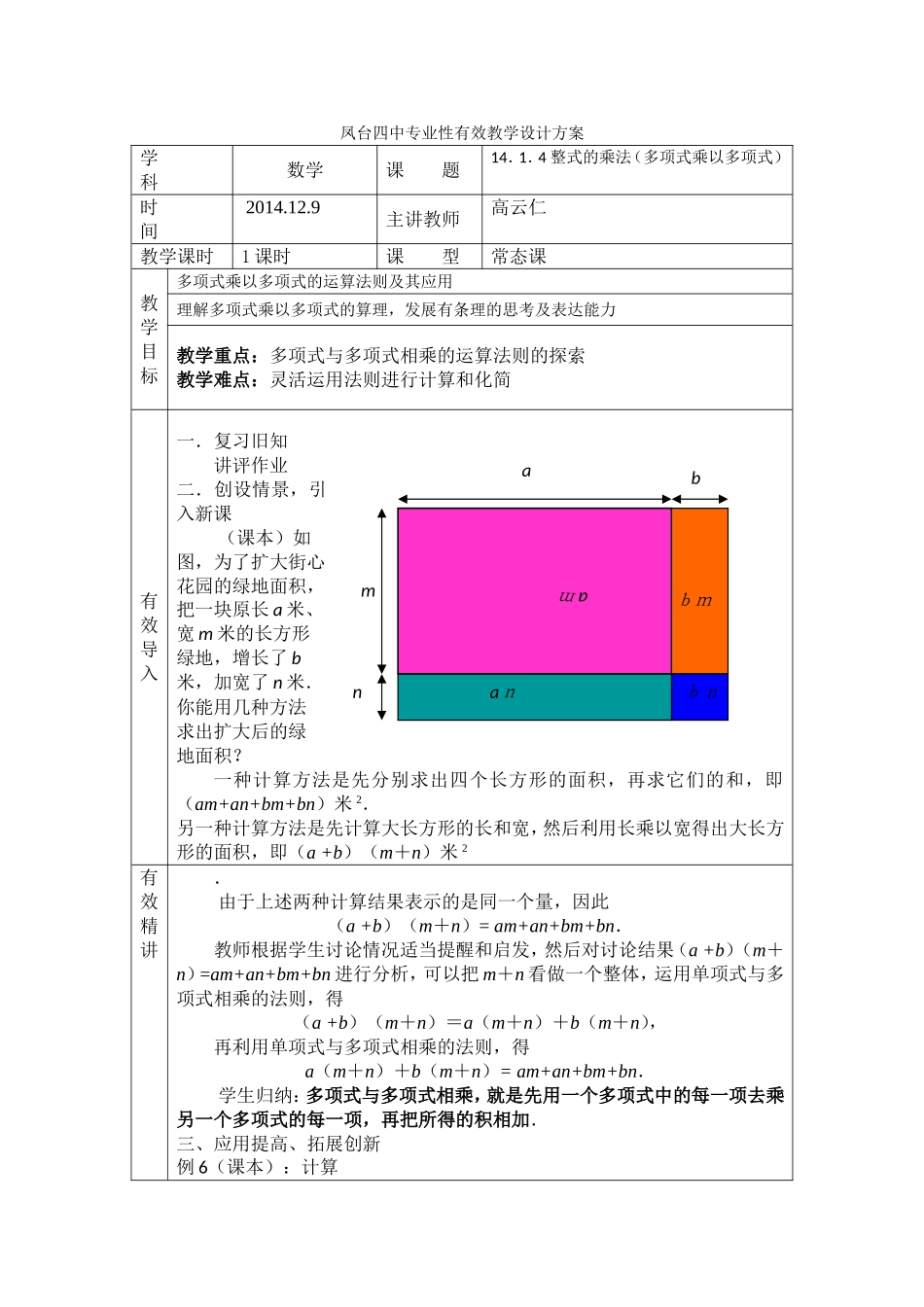
凤台四中专业性有效教学设计方案学科数学课题14.1.4整式的乘法(多项式乘以多项式)时间2014.12.9主讲教师高云仁教学课时1课时课型常态课教学目标多项式乘以多项式的运算法则及其应用理解多项式乘以多项式的算理,发展有条理的思考及表达能力教学重点:多项式与多项式相乘的运算法则的探索教学难点:灵活运用法则进行计算和化简有效导入一.复习旧知讲评作业二.创设情景,引入新课(课本)如图,为了扩大街心花园的绿地面积,把一块原长a米、宽m米的长方形绿地,增长了b米,加宽了n米.你能用几种方法求出扩大后的绿地面积?一种计算方法是先分别求出四个长方形的面积,再求它们的和,即(am+an+bm+bn)米2.另一种计算方法是先计算大长方形的长和宽,然后利用长乘以宽得出大长方形的面积,即(a+b)(m+n)米2有效精讲.由于上述两种计算结果表示的是同一个量,因此(a+b)(m+n)=am+an+bm+bn.教师根据学生讨论情况适当提醒和启发,然后对讨论结果(a+b)(m+n)=am+an+bm+bn进行分析,可以把m+n看做一个整体,运用单项式与多项式相乘的法则,得(a+b)(m+n)=a(m+n)+b(m+n),再利用单项式与多项式相乘的法则,得a(m+n)+b(m+n)=am+an+bm+bn.学生归纳:多项式与多项式相乘,就是先用一个多项式中的每一项去乘另一个多项式的每一项,再把所得的积相加.三、应用提高、拓展创新例6(课本):计算mnabbnbmaman(1)(3x+1)(x+2);(2)(x-8y)(x-y);(3)(x+y)(x2-xy+y2)进行运算时应注意:不漏不重,符号问题,合并同类项补充例题:1.(a+b)(a-b)-(a+2b)(a-b)2.(3x4-3x2+1)(x4+x2-2)3.(x-1)(x+1)(x2+1)4.当a=-1/2时,求代数式(2a-b)(2a+b)+(2a-b)(b-4a)+2b(b-3a)的值有效精练练习:(课本)100页第1、2题有效小结多项式与多项式相乘,就是先用一个多项式中的每一项去乘另一个多项式的每一项,再把所得的积相加把多项式相乘的问题转化为单项式与多项式相乘的问题作业设计布置作业:P105习题14.1第5题教学后记