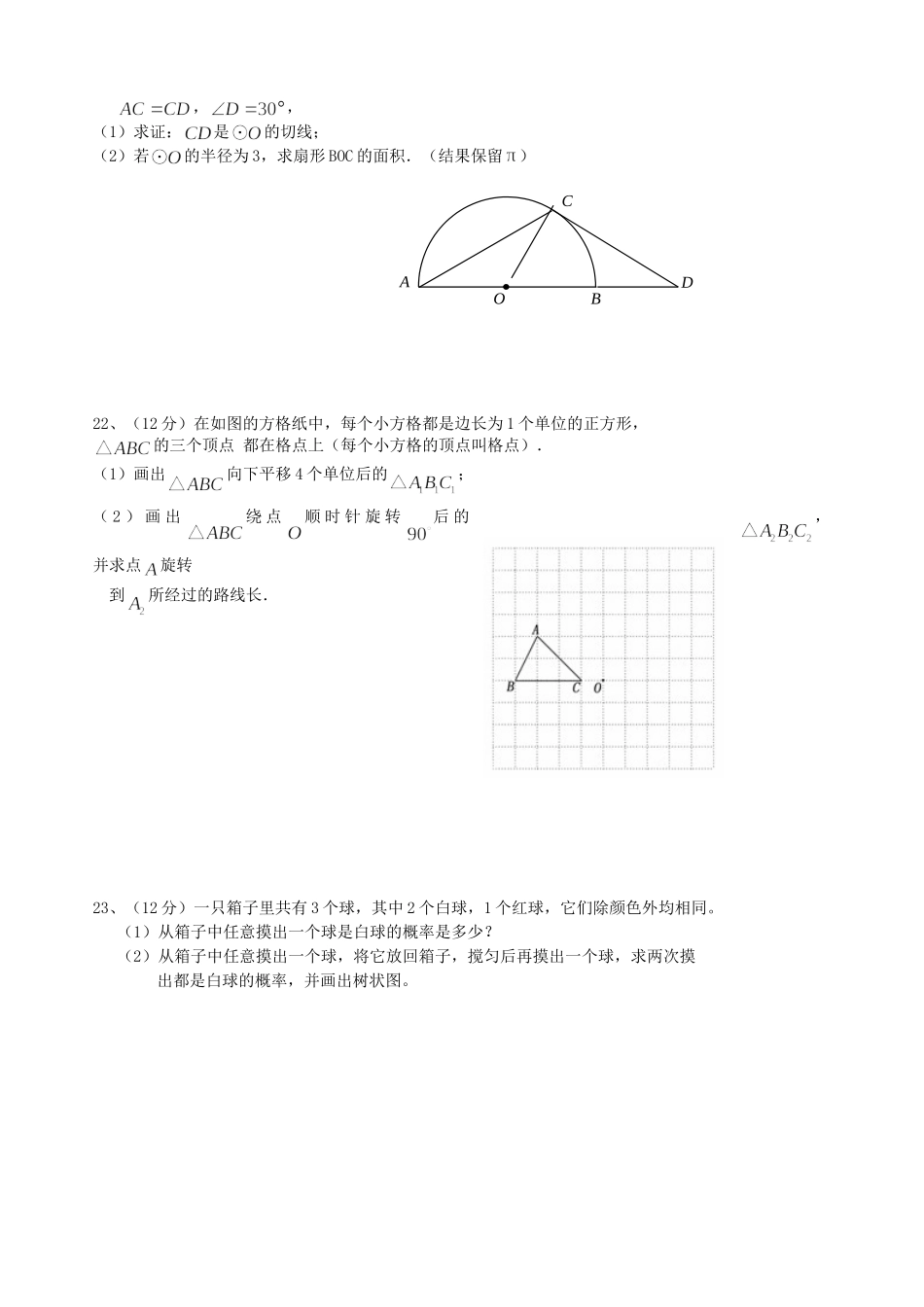
林场学校2014学年第一学期初三数学期末测试试卷1一、选择题:(每题3分,共30分,)1、一元二次方程的解是()A.B.C.,D.,2、下列事件:①明天会出太阳;②掷一枚硬币,正面向上;③地球绕着太阳转;④打开电视机,正在播足球赛.其中随机事件是()A.①②B.①③C.①④D.①②④3、一元二次方程的解是()A.0B.0或2C.2D.此方程无解4、下列图形中,是中心对称图形的是()ABCD5、下列函数中,()是二次函数。A.y=6x2+1B.y=6x+1C.y=x6+1D.y=26x+16、如果是方程的两个根,那么的值为()A.-1B.1C.2D.-27、关于x的一元二次方程的根的情况是()A.有两个不相等的实数根B.有两个相等的实数根C.没有实数根D.无法确定8、如图,点都在⊙O上,若,则的度数为()A.B.C.D.9、已知是一元二次方程的一个解,则的值是()A.-3B.3C.0D.0或310、圆锥的底面直径为8,高为3,则该圆锥的表面积为().A.36πB.48πC.72πD.144π二、填空题(每题3分,共18分)11、方程有一个实数根是2,那么。12、抛物线的开口,对称轴是,顶点坐标是,13、如图,点P是半径为5的⊙O内的一点,且OP=3,且弦AB⊥OP,则AB=________。14.布袋中装有1个红球,2个白球,3个黑球,它们除颜色外完全相同,OCBA从袋中任意摸出一个球,摸出的球是白球的概率是.15.如图,Rt△ABC中,.则△ABC的内切圆半径______.16、若正六边形的边长为2cm,则此正六边形的半径为。三、解答题(共102分)17、(12分,每小题6分)⑴解方程:⑵解方程:18、(10分)若关于x的一元二次方程有两个不相等的实数根,求实数k的取值范围。19、(10分)已知二次函数的图象经过点A(0,-1)、B(1,0)、C(-1,2);求出二次函数的关系式.20、(10分)某市为进一步创建卫生文明城市,2012年市政府对市区绿化工程投入的资金是2000万元,2014年投入的资金是2420万元,设两年间每年投入资金的年平均增长率相同。求该市对市区绿化工程投入资金的年平均增长率;21、(12分)如图,点在的直径的延长线上,点在上,AOBDC,,(1)求证:是的切线;(2)若的半径为3,求扇形BOC的面积.(结果保留)22、(12分)在如图的方格纸中,每个小方格都是边长为1个单位的正方形,的三个顶点都在格点上(每个小方格的顶点叫格点).(1)画出向下平移4个单位后的;(2)画出绕点顺时针旋转后的,并求点旋转到所经过的路线长.23、(12分)一只箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同。(1)从箱子中任意摸出一个球是白球的概率是多少?(2)从箱子中任意摸出一个球,将它放回箱子,搅匀后再摸出一个球,求两次摸出都是白球的概率,并画出树状图。24.(12分)如图,△ABC内接于半圆,AB是直径,过A作直线MN,若∠MAC=∠ABC.(1)求证:MN是半圆的切线;(2)设D是弧AC的中点,连结BD交AC于G,过D作DE⊥AB于E,交AC于F.求证:FD=FG.25、(12分)已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.(1)求证:EG=CG;(2)将图①中△BEF绕B点逆时针旋转45º,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)FBADCEG第25题图①DFBADCEG第25题图②FBACE第25题图③