最新人教版2722相似三角形的性质VIP免费

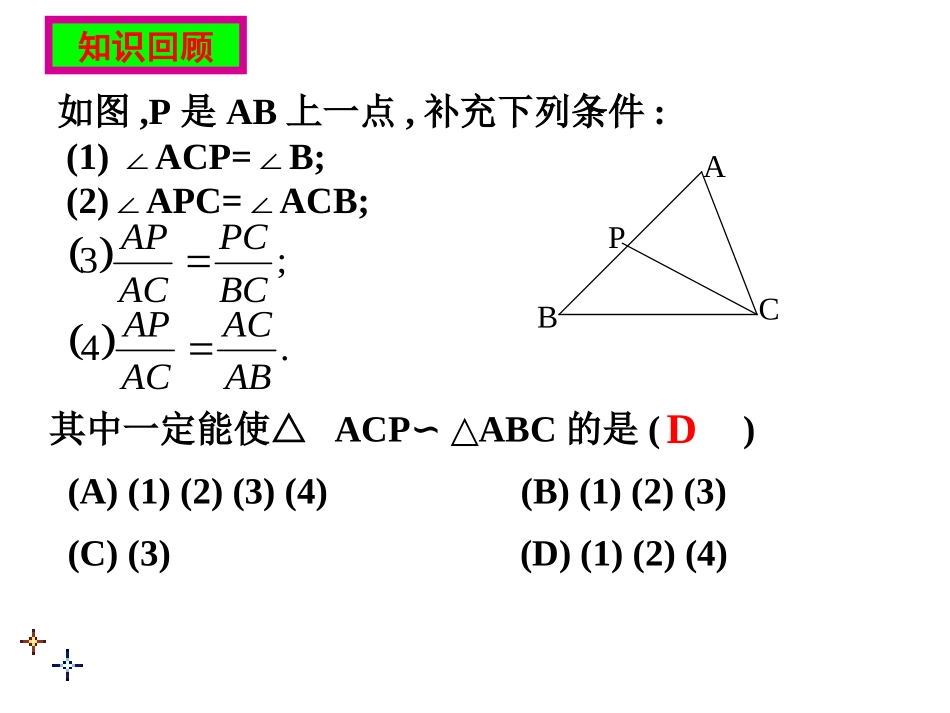
相似三角形的判定方法有那些？5.“两角”定理：两角分别相等的两个三角形相似.2.“平行”定理：平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似.3.“三边”定理：三边成比例的两个三角形相似.4.“两边夹角”定理：两边成比例且夹角相等的两个三角形相似.知识回顾1.定义判定法对应角相等对应边成比例（不常用）（不常用）6.斜边和一条直角边成比例的两个直角三角形相似.6.斜边和一条直角边成比例的两个直角三角形相似.（SSS）（SAS）（AA）（HL）2.相似三角形的性质：对应角相等，对应边成比例.如图,P是AB上一点,补充下列条件:(1)ACP=B;∠∠(2)APC=ACB;∠∠其中一定能使△ACPABC∽△的是()(A)(1)(2)(3)(4)(B)(1)(2)(3)(C)(3)(D)(1)(2)(4);3BCPCACAP.4ABACACAPABCPD知识回顾1.1.三角形中，除了三条边的长度，三个内角的角度外，三角形中，除了三条边的长度，三个内角的角度外，还有哪些几何量？还有哪些几何量？高角平分线中线新课导入想一想：（1）高、中线、角平分线的长度;2.如果两个三角形相似，那么以上这些几何量之间有什么关系呢？（2）周长、面积.ABCA'B'C'D'D如图，已知△ABC∽△A'B'C'，相似比为k，它们对应高的比是多少？分别作△ABC和△A'B'C'的对应高AD和A'D'．∴∠B＝∠B'kBAABDAAD'''' △ABC∽△A'B'C'∴Rt△ABDRt∽△A'B'D'探究：相似三角形对应高的比——等于相似比问题：解：则∠ADB=∠A'D'B'=o90根据以上探究，你能得出什么结论？相似三角形的性质1：相似三角形对应高的比等于相似比.A'B'C'E'ABCE你能仿照前面的方法证明吗？探究：相似三角形对应中线的比——等于相似比如图，已知△ABC∽△A'B'C'相似比为k，它们对应中线的比是多少？问题：分别作△ABC和△A'B'C'的对应中线AE和A'E'．解：根据以上探究，你能得出什么结论？相似三角形的性质2：相似三角形对应中线的比等于相似比.A'B'C'F'ABCF探究：相似三角形对应角平分线的比——等于相似比如图，已知△ABC∽△A‘B’C‘相似比为k，它们对应角平分线的比是多少？问题：分别作△ABC和△A'B'C'的对应角平分线AF和A'F'．解：你能仿照前面的方法证明吗？根据以上探究，你能得出什么结论？相似三角形的性质3：相似三角形对应角平分线的比等于相似比. △ABC∽△A'B'C'kACCACBBCBAAB'''''''','',''ACkCACBkBCBAkABkACCBBAAkCCkBBkAACCBBACABAABllCBAABC'''''''''''''''''''''A'B'C'ABC探究：相似三角形周长的比——等于相似比如图，已知△ABC∽△A‘B’C‘，相似比为k，它们的周长的比是多少？问题：解：根据以上探究，你能得出什么结论？相似三角形的性质4：相似三角形周长的比等于相似比.如图，已知△ABC∽△A‘B’C‘，相似比为k，它们面积的比与相似比有什么关系？ABCA'B'C'D'D分别作出△ABC和△A‘B’C‘的对应高AD和A'D'． △ABC∽△A‘B’C‘，''''2121'''DACBADBCSSCBAABC△△探究：相似三角形面积的比——等于相似比的平方问题：解：.''''2kkkDAADCBBCkCBBCDAAD''''根据以上探究，你能得出什么结论？相似三角形的性质5：相似三角形面积的比等于相似比的平方.可以记为：相似三角形对应高的比、对应中线的比、对应角平分线的比、周长的比等于相似比.归纳：相似三角形的性质相似三角形的性质：1.对应角相等.2.对应边成比例.3.对应高的比等于相似比.4.对应中线的比等于相似比.5.对应角平分线的比等于相似比.6.周长的比等于相似比.7.面积的比等于相似比的平方.还可以记为：相似三角形对应线段的比等于相似比.注意：面积的比等于相似比的平方.填空：（1）一个三角形的各边长扩大为原来的5倍，这个三角形的周长扩大为原来的（）倍；（2）一个三角形的各边长扩大为原来的9倍，这个三角形的面积扩大为原来的（）倍．练习15811.已知ΔABC与ΔA’B’C’的相似比为2：3，则周长比为，对应边上中线之比，面积之比为。2.如果两个相似三角形的面积之比为1:9，则它们对应边的比为____，对应角平分线的比为_____，周长的比为______。3.如果两个相似三角形的面积之比为2:7，较大三角形一边上的高为7，则...