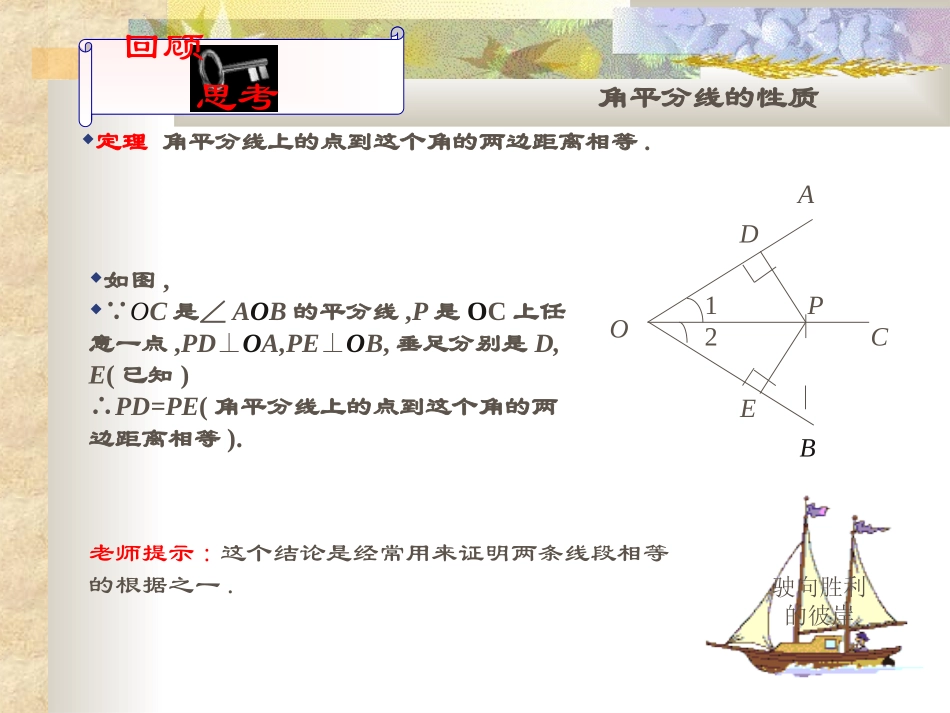
1.4角平分线(2)三角形的内心尺规作图角平分线的作法做一做11已知:∠AOB,如图.求作:射线OC,使∠AOC=∠BOC.作法:用尺规作角的平分线.1.在OAT和OB上截取OD,OE,使OD=OE.2.分别以点D和E为圆心,以大于DE/2长为半径作弧,两弧在∠AOB内交于点C.3.作射线OC.请你说明OC为什么是∠AOB的平分线,并与同伴进行交流.老师提示:作角平分线是最基本的尺规作图,这种方法要扎实掌握.C则射线OC就是∠AOB的平分线.ABODE驶向胜利的彼岸角平分线的性质定理角平分线上的点到这个角的两边距离相等.老师提示:这个结论是经常用来证明两条线段相等的根据之一.如图, OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别是D,E(已知)∴PD=PE(角平分线上的点到这个角的两边距离相等).回顾思考OCB1A2PDE驶向胜利的彼岸角平分线性质定理的逆定理逆定理在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上.如图, PA=PB,PD⊥OA,PE⊥OB,垂足分别是D,E(已知),∴点P在∠AOB的平分线上.(在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上).老师提示:这个结论又是经常用来证明点在直线上(或直线经过某一点)的根据之一.从这个结果出发,你还能联想到什么?回顾思考OCB1A2PDE驶向胜利的彼岸亲历知识的发生和发展剪一个三角形纸片通过折叠找出每个角的平分线.结论:三角形三个角的平分线相交于一点.老师期望:你能写出规范的证明过程.你想证明这个命题吗?观察这三条角平分线,你发现了什么?做一做11驶向胜利的彼岸亲历知识的发生和发展利用尺规作出三角形三条边的垂直平分线.结论:三角形三条边的垂直平分线相交于一点.老师期望:你能写出规范的证明过程.你想证明这个命题吗?你能证明这个命题吗?做一做22再观察这三条垂直平分线,你又发现了什么?与同伴交流.驶向胜利的彼岸思考分析命题:三角形三个角的平分线相交于一点.如图,设△ABC的角平分线BM,CN相交于点P,过点P分别作BC,AC,AB的垂线,垂足分别是E,F,D. BM是△ABC的角平分线,点P在BM上,∴△ABC的三条角平分线相交于一点P.咋证三条直线交于一点基本想法是这样的:我们知道,两条直线相交只有一个交点.要想证明三条直线相交于一点,只要能证明两条直线的交点在第三条直线上即可.这时可以考虑前面刚刚学到的逆定理.ABCPMNDEF∴PD=PE(角平分线上的点到这个角的两边距离相等).同理,PE=PF.∴PD=PF.∴点P在∠BAC的平分线上(在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上).驶向胜利的彼岸定理:三角形的三条角平分线相交于一点,并且这一点到三边的距离相等.如图,在△ABC中, BM,CN,AH分别是△ABC的三条角平分线,且PD⊥AB,PE⊥BC,PF⊥AC(已知),∴BM,CN,AH相交于一点P,且PD=PE=PF(三角形的三条角平分线相交于一点,并且这一点到三边的距离相等).老师提示:这又是一个证明三条直线交于一点的根据之一这个交点叫做三角形的内心.几何的三种语言ABCPMNDEF开启智慧挑战自我驶向胜利的彼岸如图,在△ABC中,已知AC=BC,∠C=900,AD是△ABC的角平分线,DE⊥AB,垂足为E.老师期望:你能正确地解答并规范地写出其过程.(1)如果CD=4cm,AC的长;(2)求证:AB=AC+CD.EDABC典例精析梦想成真试一试111.如图,已知△ABC,作△ABC一个内角和与它不相邻的两个外角的平分线,看它们是否交于一点?这样的点有几个?如果以这个点为圆心,这一点到三角形一边的距离为半径作圆,你能作出这个图形吗?ABC老师提示:三角形一个内角和与它不相邻的两个外角的平分线交于一点,这个的点叫做三角形的傍心.这样点有三个.回味无穷定理角平分线上的点到这个角的两边距离相等.逆定理在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上.定理:三角形的三条角平分线相交于一点,并且这一点到三边的距离相等(这个交点叫做三角形的内心).三角形一个内角和与它不相邻的两个外角的平分线交于一点,这个的点叫做三角形的傍心.这样点有三个.小结拓展OCB1A2PDE知识的升华独立作业习题1.91,2,3题.祝你成功!独立作业11驶向胜利的彼岸1.已知:如图,∠C=900,∠B=300,AD是Rt△ABC的角平分线.求证:BD=2CD.老师期望:你能写出规范的证明过程.ABCD独立作业2...