多项式乘以多项式VIP免费

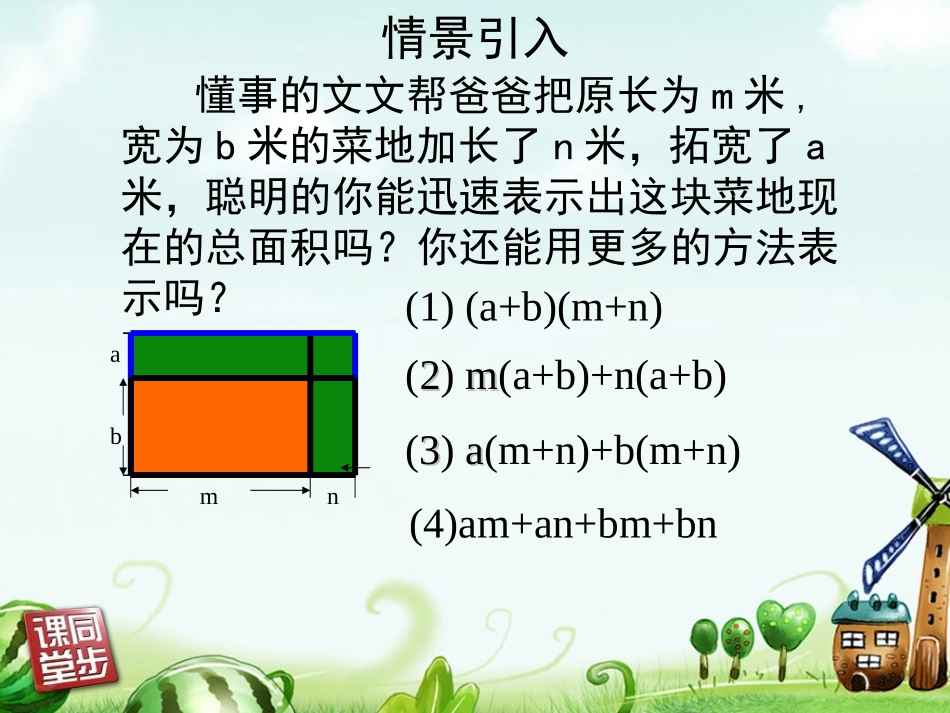
华东师大版八年级数学上册§13.2.3多项式乘以多项式懂事的文文帮爸爸把原长为m米,宽为b米的菜地加长了n米，拓宽了a米，聪明的你能迅速表示出这块菜地现在的总面积吗？你还能用更多的方法表示吗？bmna(1)(a+b)(m+n)(22)mm(a+b)+n(a+b)(33)aa(m+n)+b(m+n)(4)am+an+bm+bn情景引入懂事的文文帮爸爸把原长为m米宽为b米的菜地加长了n米，拓宽了a米，聪明的你能迅速表示出这块菜地现在的总面积吗？你还能用更多的方法表示吗？bmna(a+b)(m+n)＝＝mm(a+b)+n(a+b)＝＝aa(m+n)+b(m+n)＝＝am+an+bm+bn相信爱动脑筋的你肯定能用乘法的运算定律和单项式与多项式相乘这些原有的知识，来解释下面式子的变形过程。bmna(a+b)(m+n)＝＝mm(a+b)+n(a+b)＝＝aa(m+n)+b(m+n)＝＝am+an+bm+bn(a+b)(m+n)=am+an+bm+bn多项式的乘法法则：多项式的乘法法则：多项式与多项式相乘，先用一个多项式的每一项分别乘以另一个多项式的每一项，再把所得的积相加。(a+b)(m+n)a+b)(m+n)＝＝am+an+bm+bnam+an+bm+bn新知探究((aa++bb))XX==当当XX==mm++nn时时,(,(aa++bb))XX=?=?((aa++bb)()(mm+n)+n)=?=?+an计算：)3)(2(xx（1）（2）)12)(13(xx1234(a+b)(m+n)=am1234+bm+bn直接利用：多项式乘以多项式的法则(1)(2)(3)(3)22(3)xxxxxx参考解答：2326xxx2(2)(31)(21)3231216321xxxxxxxxx261xx26xx巩固练习yxyx73)1(yyxyyxxx7337原式:解222137yxyxyx22214yxyxyxyx2352)2(yyxyyxxx25352232原式:解22101546yxyxyx2210116yxyx65)3(xx4343)4(xx30112xx1692x6556xxxx原式:解30562xxx44343433xxxx原式:解16121292xxx计算：学一学学一学(x+y)(2x-xy+3y)(x+y)(2x-xy+3y)综合运用辨一辨辨一辨2)1()2)(32(xxx判别下列解法是否正确，若错请说出理由。解：原式)1)(1(6422xxxx)12(64222xxxx1264222xxxx522xx-3x辨一辨辨一辨2)1()2)(32(xxx判别下列解法是否正确，若错请说出理由。解：原式)1)(1(63422xxxxx1267222xxxx792xx255xx-(x2-2x+1)先化简，再求值：2223929yyyyy2y215981yy215298122原式时当，y33222261892781yyyyyy原式:解33222269182781yyyyyy2215298139其中填空：____)3)(2(2xxxx____)3)(2(2xxxx____)3)(2(2xxxx____)3)(2(2xxxx__________))((2xxbxax观察上面四个等式，你能发现什么规律？)(baab你能根据这个规律解决下面的问题吗？561(-6)(-1)(-6)(-5)62(7)(5)____xxxx－＋口答：2（－）（－35）拓展训练拓展训练这节课你有哪些收获？课堂小结