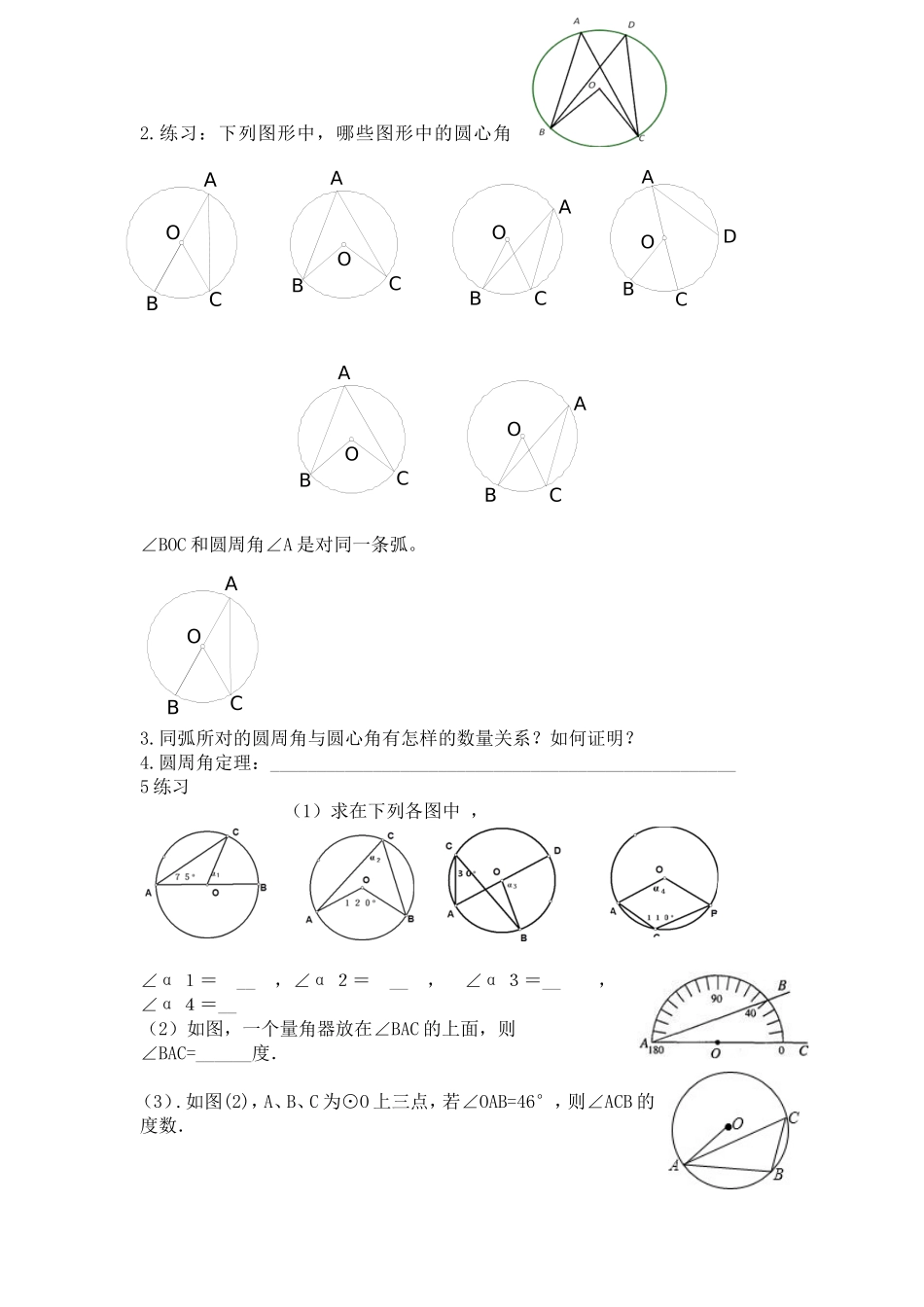
28.3圆心角和圆周角(2)导学案毛庄初中檀红涛【学习目标1、理解并掌握圆周角的概念。2、掌握圆周角定理和推论。3、经历探索圆周角的性质的过程。4、运用圆周角定理和推论进行相关计算、证明。5、体会分类、归纳等数学思想方法【导学过程】一、创设情景引入新课当球员在B,D,E处射门时,在哪个点最合适呢?二、教学过程(一)复习提问请说说我们是如何给圆心角下定义的,试回答?__在__的角叫圆心角。(二)圆周角定义:1.了解圆周角定义__在圆上,并且两边都和圆__的角叫做圆周角.2.认识圆周角判断下列各图中,哪些是圆周角?(三).探究圆周角定理1.认识同弧所对的圆周角和圆心角有没有圆周角?有没有圆心角?它们有什么共同的特点?ABCABCCABCABCO2.练习:下列图形中,哪些图形中的圆心角∠BOC和圆周角∠A是对同一条弧。3.同弧所对的圆周角与圆心角有怎样的数量关系?如何证明?4.圆周角定理:__________________________________________________5练习(1)求在下列各图中,∠α1=__,∠α2=__,∠α3=__,∠α4=__(2)如图,一个量角器放在∠BAC的上面,则∠BAC=______度.(3).如图(2),A、B、C为⊙O上三点,若∠OAB=46°,则∠ACB的度数.ABCOABCOABCOABCOABCOABCOABCOD(四).同弧所对的圆周角的关系1.探究同弧所对的圆周角的关系(1)一条弧所对的圆周角之间有什么关系?(2)结论:同弧所对的圆周角的_____2.练习(1)当球在B,D,E处射门时,在哪个呢?(2)、如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中哪些是相等的角?(3)如图,△ABC是等边三角形,动点P在圆周的劣弧AB上,且不与A、B重合,则∠BPC等于____(五).直径所对的圆周角的特殊性1.探究特殊性2.结论:直径所对的圆周角是______,90°的圆周角所对的弦是______.3基础训练(1)使用直角钢尺检查某一工件是否恰好是半圆形的凹面,成半圆形的为合格,下列四种情况中合格的是()A.B.C.D.(2).如图,若AB是⊙O的直径,AB=10cm,∠CAB=30°,则BC=_____cm.A.3B.4C.5D.8(六)走进中考1.AB是⊙O的直径,∠BCD=30°,则∠ABD=__2.如图(2)AB是⊙O的直径,C,D是圆上的两点,若∠ABD=40°,则∠BCD=3.如图(3),AB是⊙O的直径,C、D是圆上的两点.COSD=,若BC=8,则AB的长为______.三、归纳总结1、学生总结本节课学到的知识?2、学生总结学到了哪些数学方法?四、课后提升1.如图,A、B、C、D四点都在⊙O上,AD是⊙O的直径,且AD=6cm,∠ABC=∠CAD,求弦AC的长.2.(1).△ABC内接于圆O,AD为BC边上的高,若AB=3cm,AC=4cm,AD=2.5cm,求圆O的半径(2).△ABC的三顶点均在⊙O上,若∠AOC=160°,则∠ABC的度数是()A.80°B.160°C.100°D.80°或100°(3).如图,在平面直角坐标系中,⊙A经过原点O,并且分别与x轴、y轴交于B,C两点(3).如图,AB是⊙O的直径,BD是弦,延长BD到C,使DC=BD,AC与AB的大小有什么关系?为什么?,已知B(8,0),C(0,6),则⊙A的半径为()