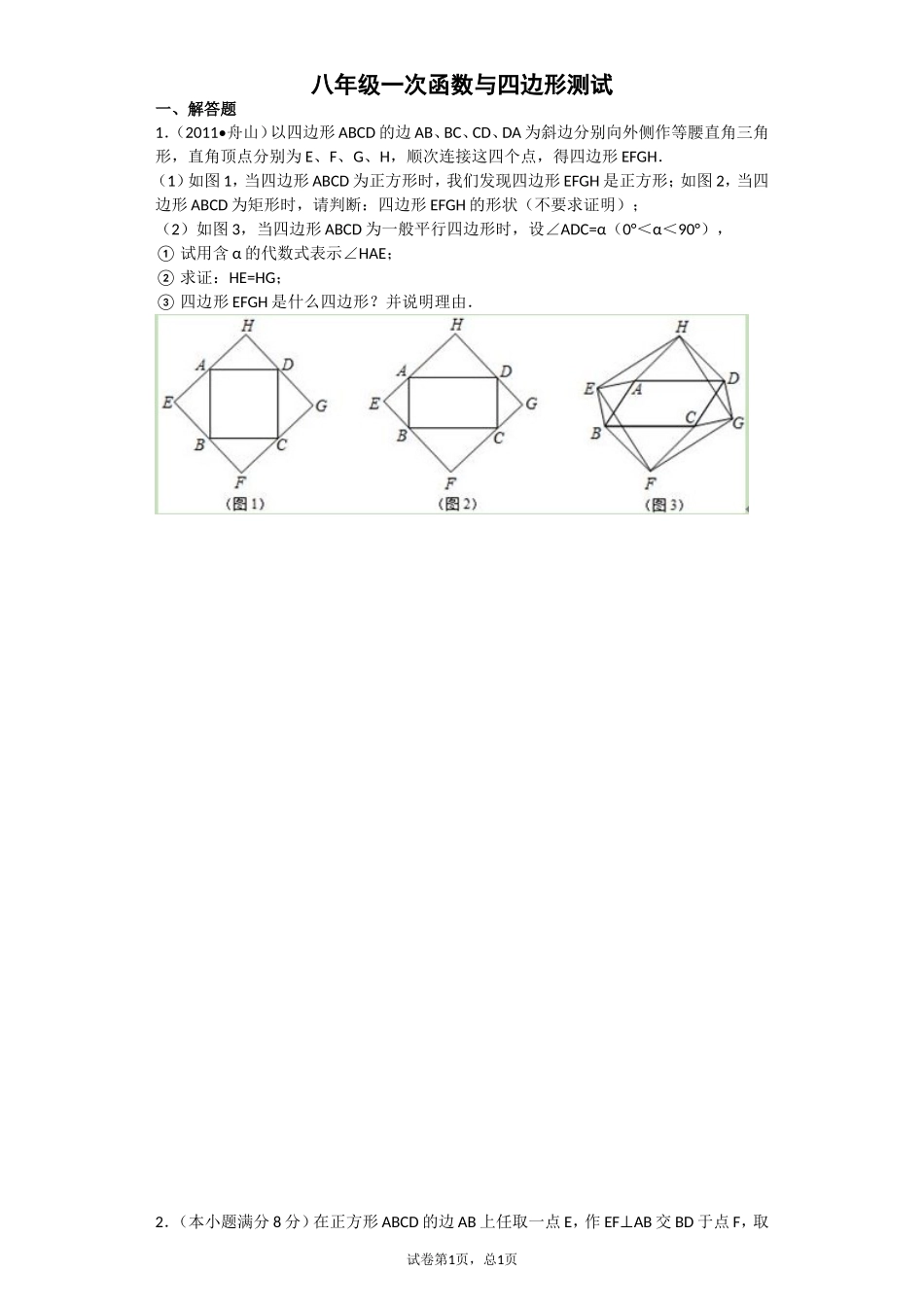
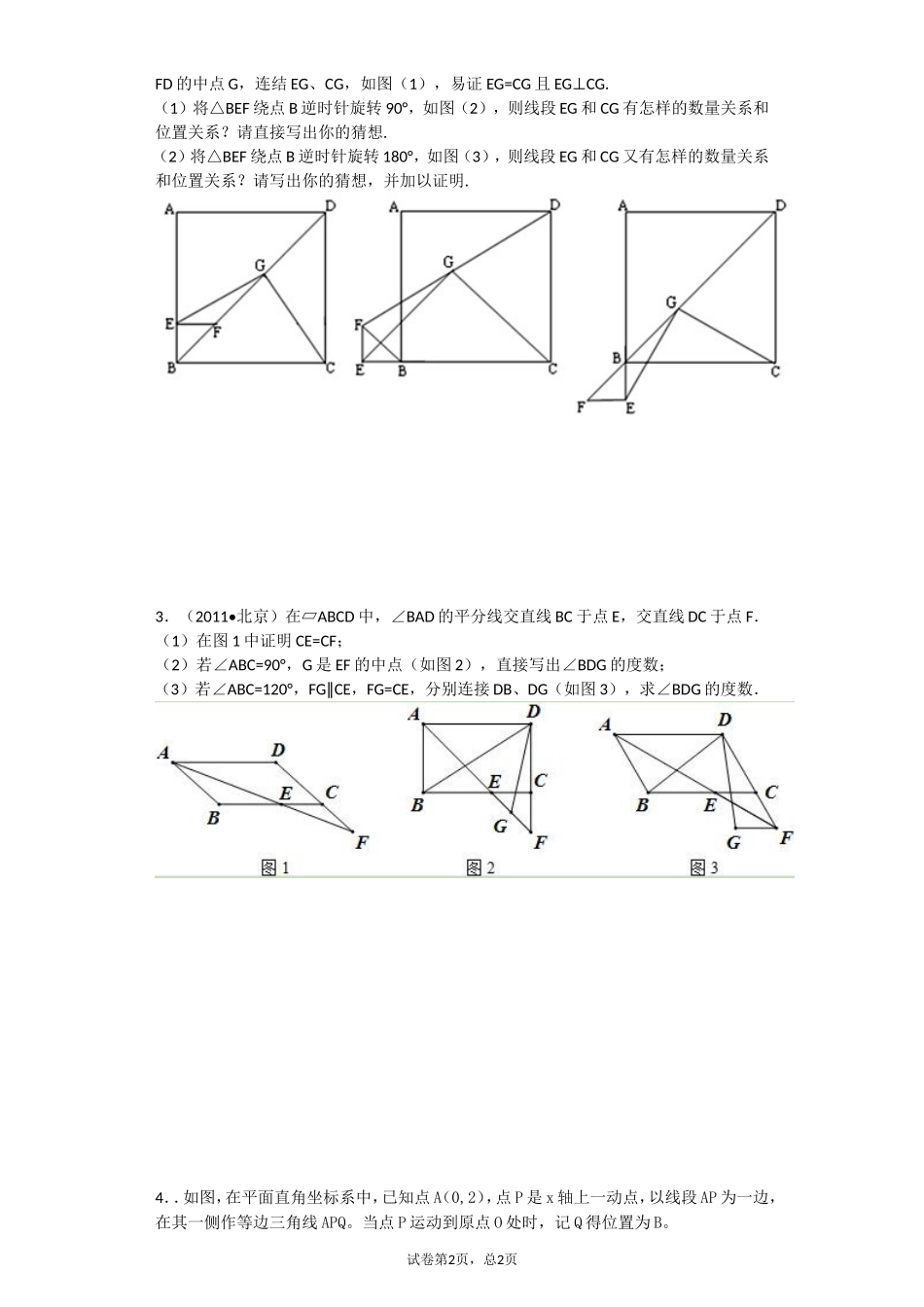
八年级一次函数与四边形测试一、解答题1.(2011•舟山)以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连接这四个点,得四边形EFGH.(1)如图1,当四边形ABCD为正方形时,我们发现四边形EFGH是正方形;如图2,当四边形ABCD为矩形时,请判断:四边形EFGH的形状(不要求证明);(2)如图3,当四边形ABCD为一般平行四边形时,设∠ADC=α(0°<α<90°),①试用含α的代数式表示∠HAE;②求证:HE=HG;③四边形EFGH是什么四边形?并说明理由.2.(本小题满分8分)在正方形ABCD的边AB上任取一点E,作EFAB⊥交BD于点F,取试卷第1页,总1页FD的中点G,连结EG、CG,如图(1),易证EG=CG且EGCG.⊥(1)将△BEF绕点B逆时针旋转90°,如图(2),则线段EG和CG有怎样的数量关系和位置关系?请直接写出你的猜想.(2)将△BEF绕点B逆时针旋转180°,如图(3),则线段EG和CG又有怎样的数量关系和位置关系?请写出你的猜想,并加以证明.3.(2011•北京)在▱ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.(1)在图1中证明CE=CF;(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;(3)若∠ABC=120°,FGCE∥,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.4..如图,在平面直角坐标系中,已知点A(0,2),点P是x轴上一动点,以线段AP为一边,在其一侧作等边三角线APQ。当点P运动到原点O处时,记Q得位置为B。试卷第2页,总2页(1)求点B的坐标;(2)求证:当点P在x轴上运动(P不与Q重合)时,∠ABQ为定值;(3)是否存在点P,使得以A、O、Q、B为顶点的四边形是梯形?若存在,请求出P点的坐标;若不存在,请说明理由。5.已知:如图,O正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连结DF,交BE的延长线于点G,连结OG.(1)说明:△BCE≌△DCF;(2)OG与BF有什么数量关系?说明你的结论;(3)若BC·BD=,求正方形ABCD的面积.6.如图1,在平面直角坐标系中,直线AB与轴交于点A,与轴交于点B,与直线OC:交于点C.试卷第1页,总1页(1)若直线AB解析式为,①求点C的坐标;②求△OAC的面积.如图2,作的平分线ON,若AB⊥ON,垂足为E,△OAC的面积为6,且OA=4,P、Q分别为线段OA、OE上的动点,连结AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.7.如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(-3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H。(1)求直线AC的解析式;(2)连接BM,如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设PMB的面积为)0(SS,点P的运动时间为t秒,求S与t之间的函数试卷第2页,总2页关系式(要求写出自变量t的取值范围);8.如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标(3,3),将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.试卷第1页,总1页(1)求证:△AOG≌△ADG;(2)求∠PAG的度数;并判断线段OG、PG、BP之间的数量关系,说明理由;(3)当∠1=∠2时,求直线PE的解析式.试卷第2页,总2页参考答案1.(1)答:四边形EFGH的形状是正方形.(2)解:①∠HAE=90°+a,在平行四边形ABCD中ABCD∥,BAD=180°ADC=180°a∴∠﹣∠﹣,HAD △和△EAB是等腰直角三角形,HAD=EAB=45°∴∠∠,HAE=360°HADEABBAD=360°45°45°∴∠﹣∠﹣∠﹣∠﹣﹣﹣(180°a﹣)=90°+a,答:用含α的代数式表示∠HAE是90°+a.②证明: △AEB和△DGC是等腰直角三角形,AE=AB∴,DC=CD,在平行四边形ABCD中,AB=CD,AE=DG∴,HAD △和△GDC是等腰直角三角形,HDA=CDG=45°∴∠∠,HDG=HDA+ADC+CDG=90°+a=HAE∴∠∠∠∠∠,HAD △是等腰直角三角形,HA=HD∴,HAEHDC∴△≌△,HE=HG∴.③答:四边形EFGH是正方形,理由是:由②同理可得:GH=GF,FG=FE,HE=HG ,GH=GF=EF=HE∴,∴四边形EFGH是菱形,HAEHDG △≌△,DHG=AHE∴∠∠,AHD=AHG+DHG=90° ∠∠∠,EH...