水文地质学第8章-3VIP免费

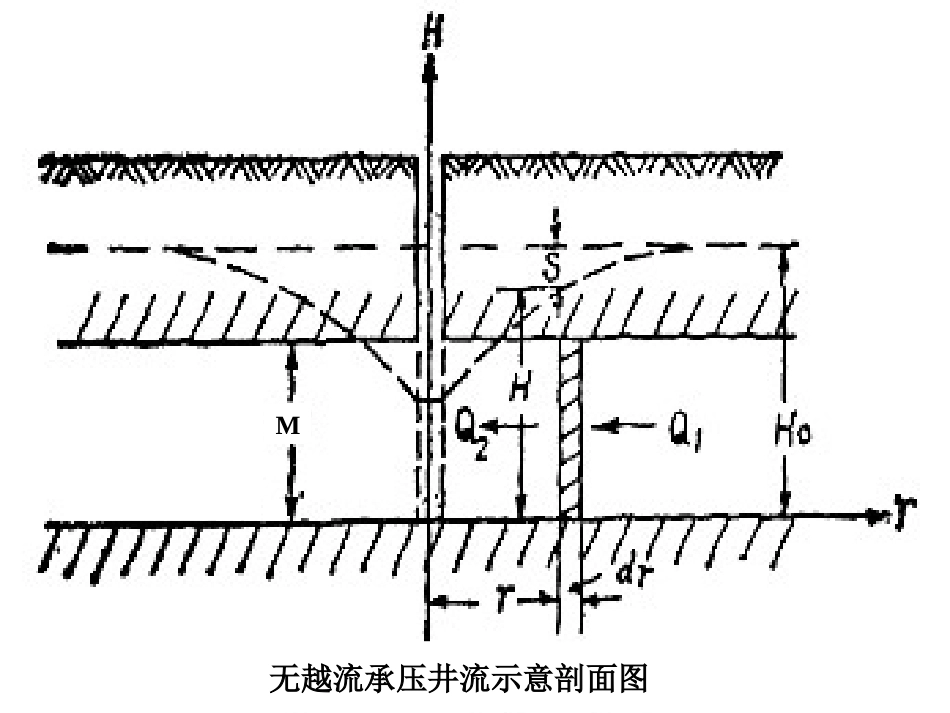
§8-7地下水非稳定井流公式一、承压水完整井非稳定流公式---泰斯公式1、泰斯公式的假定条件：（1）单井位于含水层中央，井径无限小，定流量抽水（如下图示）；（2）含水层均质、等厚、各向同性，水平埋藏且无限延伸；（3）无垂向水量交换，无侧向补给；（4）渗流符合达西定律；（5）抽水前水头面水平，水头为H0。抽水后形成以井轴为对称的降落漏斗；（6）含水层和水都具有弹性。M无越流承压井流示意剖面图方程推导：根据水均衡原理：Q1-Q2=ΔV---------------(1)根据达西定律：因为单位时间的水头下降为，则单位时间内单元含水柱体内的弹性释放水量应为)(22)(2222221rHrHrKMdrrHKMrdrrrHrKMrHrMKdrrQQQtHtHrHrrHTVQQ*1)1(2221式，化简后得：代入、、把tHrdrV*22、泰斯公式的导出：根据上述假定条件，建立数学模型：求解上述数学模型的思路：先将二阶偏微分方程变换为只含一个变量的常微分方程，求出该微分方程的解，最后得出计算公式---泰斯公式。TQrHrHHHHrHrrHTtHrt2lim1*00022r0t＞0r＞0t=0r＞0t＞0r∞t＞0duueTQsduueTQHHuuuu440W(u)值可由表中查得，根据泰斯公式就可求出承压含水层中单井抽水时任一时刻t，距离抽水井r处的水头降深值s。443322ln5772.0)1(ln5772.04321uuuuunnuuduuennnuu！！！！1432)1(ln5772.0443322ln5772.0)(nnnnnuuuuuuuuW令：！！！！TtruuWuWTQs4*)()(42泰斯井函数，泰斯公式，从W(u)的级数展开式可看出，当u值足够小时，级数第三项以后的各项数值都非常小，W(u)可用级数的前两项近似表示。将代入上式，泰斯公式变为：-----雅各布公式泰斯公式的近似表达式为雅各布公式，其近似程度作如下分析：当时，泰斯公式和雅各布公式计算结果误差；当时，误差；当时，误差。uuuW1ln781.1lnln5772.0)(Ttru4*2*25.2lg183.0*25.2lg43.2*25.2ln4)(4222rTtTQrTtTQrTtTQuWTQs*25.2lg183.02rTtTQs1.0u%505.0u%201.0u%25.0例：有一凿于宽阔承压含水层中的完整井，井径0.305m，出水量2700m3/d，含水层厚度M=30m，渗透系数K=41m/d，弹性释水系数μ*=0.00025，试求抽水4小时，距井60m处的水位降深s。解：根据题意满足泰斯公式应用条件，查表W(u)=6.2363322101.12443041400025.0604*Ttru)(09.10899.12363.6304114.342700)(4muWTQs如果用雅各布公式求解其结果为：)(09.10885.100025.060244304125.2lg30412700183.0*25.2lg183.022mrTtTQs井函数W（u）表3、泰斯公式的讨论（1）井函数W(u)的值随u的增大而减小（如下图示），当抽水井作定流量抽水时，降深s随着离抽水井距离r的增大而减小，随着抽水时间t的延长而增大。（2）水头的下降速度：把代入：水头下降速度是时间t与距离r的函数，对于同一时间t，近井轴处的下降快，远离井轴处的下降速度慢。r一定时，当t足够大时，0，1tuduueTQHutHduueTQHHuuuu4400Ttru4*2TtrTtretTQtsetTQtH4*4*221414Ttru4*2Ttre4*2则：即抽水井周围的某一范围内，水头下降的速度基本相同，与距离r无关[经过一定时间抽水后，抽水井附近的降落漏斗曲面近乎等速（幅）下降]。tTQts14（3）设通过柱形径距为r过水断面流量为Qr，当t一定时，通过各过水断面的流量随着距离r的减小而增大，因为恒为正，所以，故Qr