《绝对值》课件VIP免费

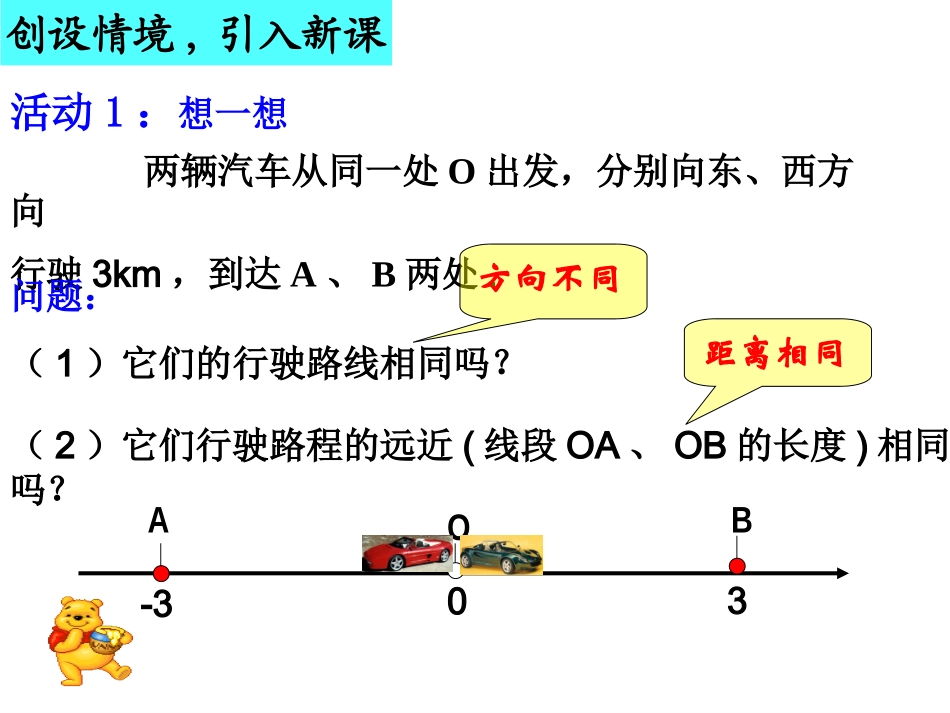
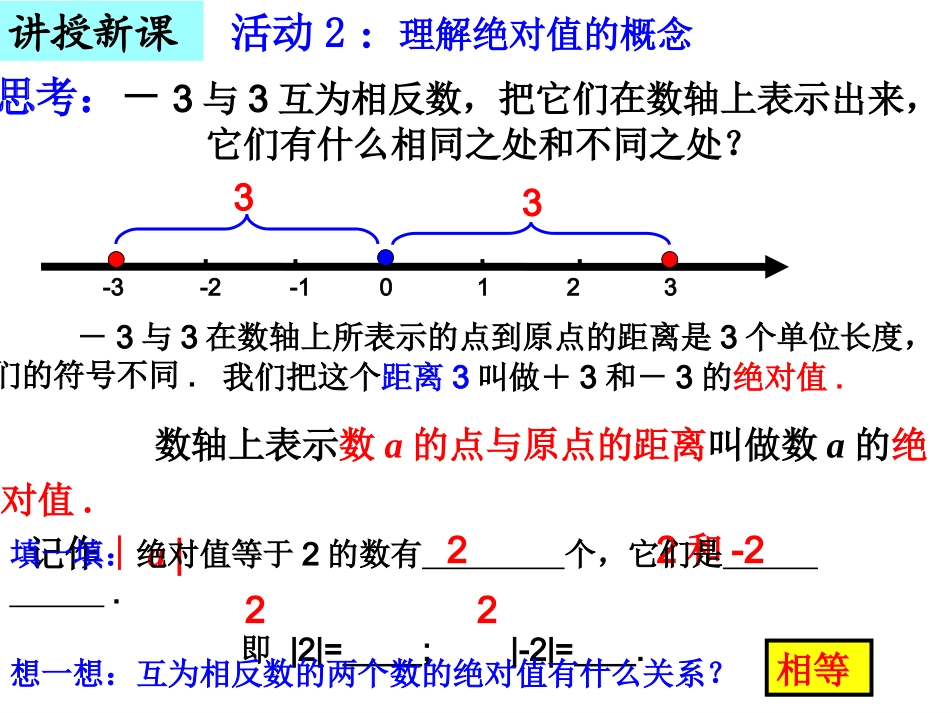
1.2.3绝对值活动1：想一想两辆汽车从同一处O出发，分别向东、西方向行驶3km，到达A、B两处.03AO-3B距离相同方向不同创设情境,引入新课问题：（1）它们的行驶路线相同吗？（2）它们行驶路程的远近(线段OA、OB的长度)相同吗？数轴上表示数a的点与原点的距离叫做数a的绝对值.记作∣a∣讲授新课32和-2-3-2-10123填一填：绝对值等于2的数有个，它们是.即|2|=;|-2|=.23思考：－3与3互为相反数，把它们在数轴上表示出来，它们有什么相同之处和不同之处？－3与3在数轴上所表示的点到原点的距离是3个单位长度，它们的符号不同.活动2：理解绝对值的概念想一想：互为相反数的两个数的绝对值有什么关系？相等22我们把这个距离3叫做＋3和－3的绝对值.12|1|=;|-1|=;|2|=;|-2|=;|5|=;|-5|=;||=;|-|=;121211口答：22550一个正数的绝对值是；它本身它的相反数0的绝对值是0.讲授新课一个负数的绝对值是，|0|=.活动2：理解绝对值的概念21议一议：(1)当a是正数时，｜a｜＝____；(2)当a=0时，｜a｜＝＿＿;(3)当a是负数时，｜a｜＝＿＿.a－a0讲授新课活动3：理解绝对值的性质绝对值具有非负性.｜a｜≥0知识应用例2如果一个数的绝对值等于，则这个数是_________．32方法总结：解答此类问题容易漏解、考虑问题不全面，所以一定要记住：绝对值等于某一个数的值有两个，它们互为相反数，0除外．例1－3的绝对值是()A．3B．－3C．D.3131A32变式练习：若|x|=2,则x=.±2活动4：例题讲解例3化简：|－8|＝______；|－(－2)|＝______－|－1.5|＝______；－（－1.5）＝______；知识应用－1.5281.5活动4：例题讲解知识应用例4若|a－3|＋|b－2015|＝0，求a，b的值.分析：由绝对值的性质可知|a－3|≥0，|b－2015|≥0，方法总结：如果几个非负数的和为0，那么这几个非负数都等于0.变式练习：（1）若|a+5|＋|b－2016|＝0，则a=，b=.（2）若|a-2019|＋|b+2016|＝0，则a+b=.-520163活动4：例题讲解由|a－3|＋|b－2015|＝0则有|a－3|=0，|b－2015|=0.例5在奥运会乒乓球比赛中用球的质量有严格的规定，下表是6个乒乓球质量检测的结果(单位：克，超过标准质量的克数记为正数，不足标准重量的克数记为负数).一号球二号球三号球四号球五号球六号球－0.50.10.20－0.08－0.15知识应用请找出三个误差相对较小一些的乒乓球，并用绝对值的知识说明．解：四号球，|0|＝0正好等于标准的质量，五号球，|－0.08|＝0.08，比标准球轻0.08克，二号球，|＋0.1|＝0.1，比标准球重0.1克．方法总结：判断质量、零件尺寸等是否合格，关键是看偏差的绝对值的大小，而与正、负数无关.活动4：例题讲解1．绝对值的定义：一般地，数轴上表示数a的点与原点的距离叫做数a的绝对值，记作|a|.2．绝对值的性质：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0.用符号表示为：知识归纳|a|＝a（a>0）0（a＝0）－a（a<0）或|a|＝a（a≥0）－a（a<0）（非负性）活动5：谈收获1、教科书第11页练习.2、练习册第10-第11页.课后作业1.写出下列各数的绝对值：0,100,112,9.3,63x03a2.若，则x=；若，则a=.3.下列说法中，错误的是（）A、一个数的绝对值一定是正数B、互为相反数的两个数的绝对值相等C、绝对值最小的数是0D、绝对值等于它本身的数是非负数4.有四包真空小包装火腿，每包以标准克数（450克）为基数，超过的克数记作正数，不足的克数记作负数，以下数据是记录结果，其中表示实际克数最接近标准克数的是（）A、+2B、-3C、+3D、+45.若014yx，则x=，y=.《绝对值》随堂检测《绝对值》随堂检测参考答案1.解：∣6=6∣，∣-3.9=3.9∣，∣100=100∣，∣0=0∣1121122.±3，33.A4.A5.x=4,y=-1.