工程图学第3章点几何元素的投影VIP免费

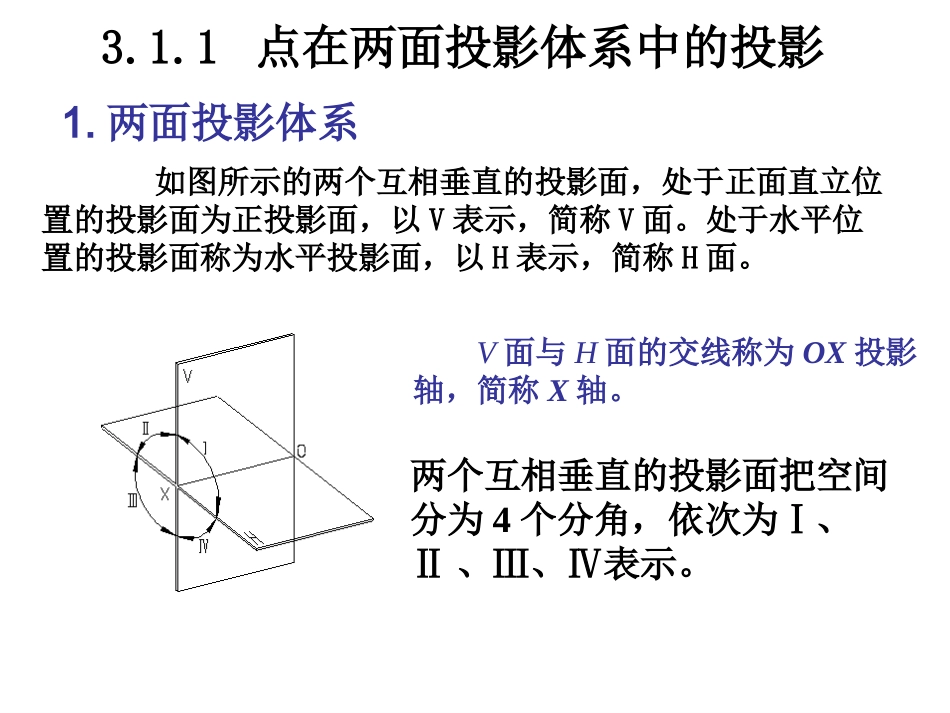
第第33章几何元素的投影章几何元素的投影3.1点的投影Pb●●AP采用多面投影过空间点A的投射线与投影面P的交点即为点A在P面上的投影。B1●B2●B3●点在一个投影面上的投影不能确定点的空间位置。点在一个投影面上的投影a●3.1.1点在两面投影体系中的投影1.两面投影体系如图所示的两个互相垂直的投影面，处于正面直立位置的投影面为正投影面，以V表示，简称V面。处于水平位置的投影面称为水平投影面，以H表示，简称H面。V面与H面的交线称为OX投影轴，简称X轴。两个互相垂直的投影面把空间分为4个分角，依次为Ⅰ、Ⅱ、Ⅲ、Ⅳ表示。2.点的两面投影图a—点A的水平投影a’—点A的正面投影展开方法：将H面绕X轴向下旋转90°3.点的两面投影规律1）点的水平投影和正面投影的连线垂直于X轴，即aaX⊥轴;2）点的水平投影到X轴的距离等于空间点到V面的距离，即aax=Aa’;3)点的正面投影到X轴的距离等于空间点到H面的距离,即a’ax=Aa.HWV3.1.23.1.2点在三投影面体系中的投影点在三投影面体系中的投影投影面◆正面投影面（简称正面或V面）◆水平投影面（简称水平面或H面）◆侧面投影面（简称侧面或W面）投影轴oXZOX轴V面与H面的交线OZ轴V面与W面的交线OY轴H面与W面的交线Y三个投影面互相垂直1.点的三面投影三个投影轴互相垂直投影轴的交点称为原点空间点A在三个投影面上的投影a点A的正面投影a点A的水平投影a点A的侧面投影空间点用大写字母表示，点的投影用小写字母或加“，”表示。WHVoXa●a●a●A●ZYWVH●●●●XYZOVHWAaaaxaazay向后翻向下翻不动投影面展开aaZaayayaXYHYWO●●az●xY轴分解为两部分——YH、YW点的三面投影和坐标的关系为：画出A点投影图和举例水平投影a反映了A点X和Y的坐标；正面投影a’反映了A点X和Z的坐标；侧面投影a”反映了A点Y和Z的坐标。yxzOAVHWa'aa"XZYaxaayz点的投影规律:①aaOX⊥轴②aaOZ⊥轴③aax=aaz●●●●XYZOVHWAaaaxaazay●●YWZazaXYHaywOaaxayHa●2.点的坐标和三面投影规律点的坐标与三面投影的关系Aa"=a'az=aay=axO=xAAa'=aax=a"az=ayO=yAAa=a'ax=a"ay=azO=zA综合点的坐标和三面投影的投影规律如下：1、a'aOX⊥，a'az=aayH=xA2、a'a"OZ⊥，a'ax=a"ayw=zA3、aax=a"az=yAZazX●●YWayHaywOaaxayHa●Y●●●●ZOVHWAaaaxaazayxzY具体作图时用45°辅助线帮助作图【例】已知A（20、15、15），作出A点的三面投影。1)作OX、OY和OZ轴，并作∠YHOYW的角平分线45º线。2)自O点沿OX轴量取20，即XA=20，得ax点。3)过ax点作OX轴的垂线，在此垂线上沿OYH轴方向量取15，即YH=15，得a点；在此垂线上沿OZ轴方向量取15，得a＇点。4)由a‘作OZ轴的垂线，交OZ轴于az,在此垂线上沿OYW轴方向量取aza″=axa=YA=15，得a″。●●aaax例：已知点的两个投影，求第三投影。例：已知点的两个投影，求第三投影。●a●●aaaxazaz解法一:通过作45°线使aaz=aax解法二:用分规直接量取aaz=aaxa●3.3.特殊投影点：特殊投影点：ddeef’fefdzxYWYH0例：已知点的两投影，求其第三投影例：已知点的两投影，求其第三投影daaa3.1.33.1.3两点的相对位置两点的相对位置两点的相对位置指两点在空间的上下、前后、左右位置关系。判断规律：▲x坐标大的在左▲y坐标大的在前▲z坐标大的在上B点在A点之前、之右、之下。baaabb●●●●●●XYHYWZ1.两点的相对位置的确定例题例题22已知已知AA点在点在BB点之前点之前55毫米，之上毫米，之上99毫米，之毫米，之右右88毫米，求毫米，求AA点的投影。点的投影。aaaXZYWYHObbb9852.重影点重影点：空间两点在某一投影面上的投影重合为一点时，则称此两点为该投影面的重影点。A、C为H面的重影点被挡住的投影加()●●●●●aacc()ac图1—9重影点的投影一点的两投影之间的连线垂直于投影轴；点的一个投影到某投影轴的距离等于空间点到与该投影轴相邻的投影面之间的距离。即a'a⊥0X；a'a"⊥0Z；aax=a”az点的三面投影规律点的一个投影反映了点的两个坐标。已知点的两个投影，则点的X、Y、Z三个坐标就可确定，即空间点是唯一确定的。因此已知一个点的任意两个...