《2413垂直于弦的直径》课件VIP免费

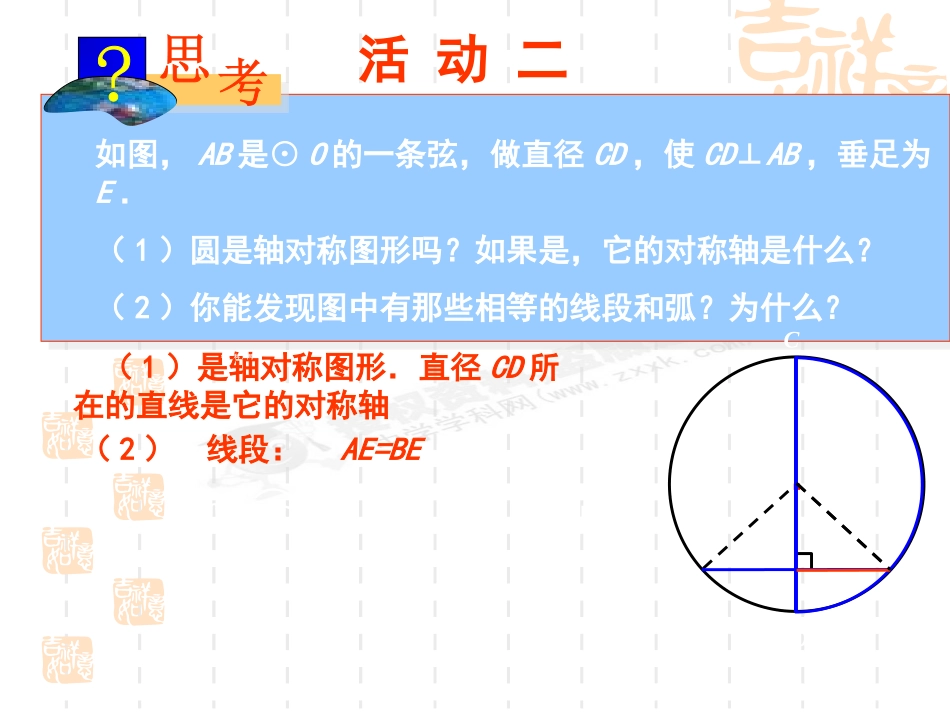
学科网实践探究沿着圆的任意一条直径对折，你发现了什么？由此你能得到什么结论？可以发现：圆是轴对称图形，任何一条直径所在直线都是它的对称轴．·如图，AB是⊙O的一条弦，做直径CD，使CD⊥AB，垂足为E．（1）圆是轴对称图形吗？如果是，它的对称轴是什么？（2）你能发现图中有那些相等的线段和弧？为什么？·OABCDE活动二（1）是轴对称图形．直径CD所在的直线是它的对称轴（2）线段：AE=BE学.科.网弧：AD=BDAC=BC︵︵︵︵·OABCDE垂径定理：AE＝BE，，ACBCADBD即直径CD平分弦AB，并且平分及ABACB经过圆心垂直于弦的直线平分弦，并且平分弦所对的两条弧．·OCDABE垂径定理：经过圆心垂直于弦的直线平分弦，并且平分弦所对的两条弧．几何语言：︵︵︵︵∵AB过圆心，AB⊥弦CD(已知)∴CE=DEBC=BDAC=AD（垂径定理）以下的能用垂径定理吗？····DOOOOCBBBABAAAEEEECCDDC∟·OCDABE垂径定理：经过圆心垂直于弦的直线平分弦，并且平分弦所对的两条弧．有5个知识点：有一条直线经过圆心这条直线垂直于一条弦这条直线平分这条弦这条直线平分这条弦所对的一条弧这条直线平分这条弦所对的另一条弧推论：过圆心平分弦（不是直径）的直线垂直于弦，并且平分弦所对的两条弧．1．如图，在⊙O中，弦AB的长为8cm，圆心O到AB的距离为3cm，求⊙O的半径．·OABE练习解：答：⊙O的半径为5cm.活动三Zx.xk根据垂径定理得482121ABAEOAOAOAOAOAOAAEOE525251694322222222222斜边直角边直角边2．如图，在⊙O中，直径AB的长为26cm，圆心O到CD的距离OM为5cm，求弦CD的长．·练习解：答：弦CD的长为24cm.活动三根据垂径定理得∟ACDBMO∵OM2+DM2=OD2∴52+DM2=13225+DM2=169DM2=144DM=12CD=2DM=243．如图，在⊙O中，弦CD的长为30cm，BM为9cm，求⊙O半径的长．·练习解：答：⊙0的半径长为17cm.活动三根据垂径定理得∟ACDBMO∵OM2+DM2=OD2∴（R-9）2+152=R2R2-18R+81+225=R2R=17306=18RDM=30÷2=15R2-R2+81+225=18R2．如图，在⊙O中，AB、AC为互相垂直且相等的两条弦，OD⊥AB于D，OE⊥AC于E，求证四边形ABOE是正方形．·OABCDE证明：OEACODABABAC909090OEAEADODA∴四边形ADOE为矩形（有三个角是直角的四边形是矩形）又∵AC=AB1122AEACADAB，∴AE=AD∴四边形ADOE为正方形.（一组邻边相等的矩形是正方形）z.xx.k根据垂径定理得