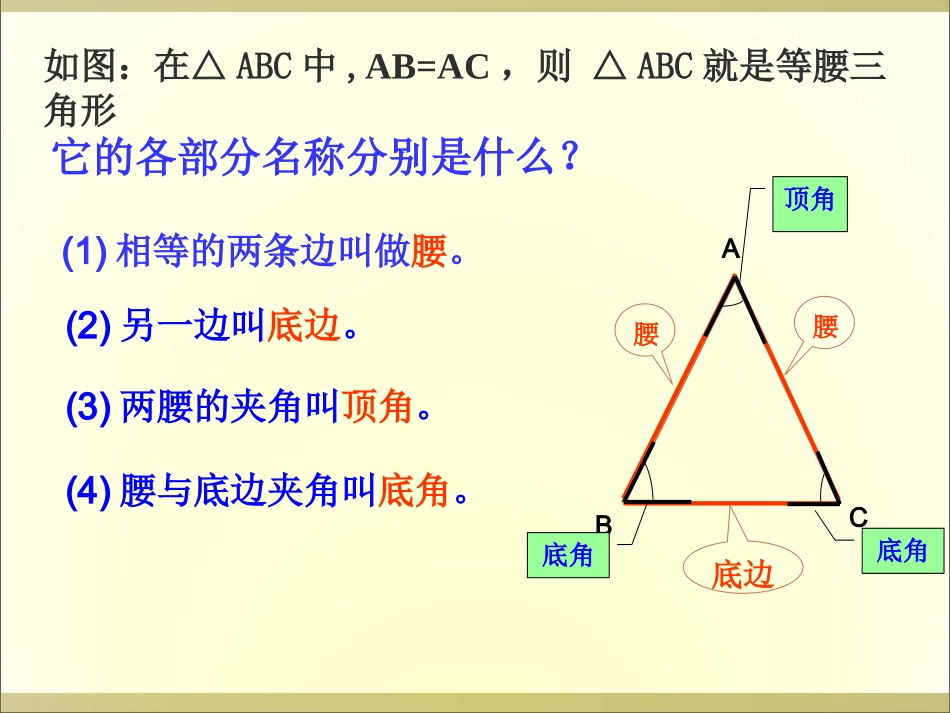
如图:在△ABC中,AB=AC,则△ABC就是等腰三角形它的各部分名称分别是什么?ABC(1)相等的两条边叫做腰。腰腰底边(2)另一边叫底边。顶角底角底角(3)两腰的夹角叫顶角。(4)腰与底边夹角叫底角。下面哪些是等腰三角形?12345达标练习一如右图,在△DEF中,DE=DF,请问:哪些边是腰?DEF底边是哪条边?顶角是哪个角?底角是哪些角?拿出你的等腰三角形纸片,把纸片折折看,让两腰AB、AC重叠在一起,折痕为AD.你能发现什么现象吗?做一做、想一想、说一说等腰三角形是一种特殊的三角形,它除具有一般三角形的性质外,还有一些特殊的性质吗?ABCD看看你本组其他同学的情况,共同交流,能得出什么结论?(1)等腰三角形是轴对称图形。(2)∠B=∠C(3)∠BAD=∠CAD,AD为顶角的平分线(4)∠ADB=∠ADC=90°AD为底边上的高(5)BD=CD,AD为底边上的中线。现象(3)、(4)、(5)能用一句话归纳出来吗?现象(2)能用一句话归纳出来吗?等腰三角形的两个底角相等等腰三角形的顶角平分线、底边上的高和底边上的中线互相重合(简称“三线合一”)现象等腰三角形的性质1、等腰三角形的两个底角相等(简称“等边对等角”)2、等腰三角形的顶角平分线、底边上的高和底边上的中线互相重合(简称“三线合一”)一般的三角形有这种性质吗?要注意是指顶角的平分线、底边上的高、底边上的中线这三线重合。.按要求做一做1.先任意做一锐角∠a2.再任画一线段BC3.然后以BC为公共边在它的同侧作∠B=a∠∠C=a∠两边交与点A4.用圆规量一量AB,AC。你发现什么结论?如果一个三角形有两个角相等,那么它们所对的边也相等(1) ADBC⊥,∴∠____=____∠,___=___(2) AD是中线,∴___⊥___,∠____=∠____(3) AD是角平分线,∴______⊥,___=___BADCADBDCDADBCADBCBADCADBDCD一:根据等腰三角形性质,在△ABC中,AB=AC时,ABCD例1已知:在△ABC中,AB=AC,∠B=80°.求∠C和∠A的度数.发散思维(1)已知:在△ABC中,AB=AC,∠A=80°.求∠B和∠C的度数.发散思维(2)已知:△ABC是等腰三角形,其中一个角为80°求另外两个角的度数.解: AB=AC∴∠C=∠B=80°()你能说出它的理由吗?等边对等角又 ∠A+∠B+∠C=180°,∴∠A=180°-80°-80°=20°.例2已知:如图,房屋的顶角∠BAC=1000,过屋顶A的立柱AD⊥BC,屋椽AB=AC。求顶架上∠B、∠C、∠BAD、∠CAD的度数。解:在△ABC中, AB=AC(已知),∴∠B=∠C(等边对等角).∴∠B=∠C=(1800-∠A)=400(三角形内角和定理).又 AD⊥BC(已知),∴∠BAD=∠CAD(等腰三角形的顶角的平分线与底边上的高互相重合).∴∠BAD=∠CAD=500.ABCD1、下列图形是否是轴对称图形,说出它的对称轴,并验证你的判断。(1)圆,(2)矩形,(3)直角梯形,(4)扇形2、如图,⊿ABC中,AB=AC,求其它角的度数ABC60°ABC90°ABC30°二、判断:4、如图1: AB=AC1=2∴∠∠()BCA⌒⌒12DE图11.等腰三角形一角的平分线,一边上的中线,一边上的高都是它的对称轴().等腰三角形的两角相等()23.三角形的高线.角平分线.中线三线合一()试一试!填空:55o、55o70o、40o55o、55o或70o、40o1、已知等腰三角形的顶角是70o,则它的其它两角的度数是。2、已知等腰三角形的底角是70o,则它的其它两角的度数是。3、已知等腰三角形的一个内角是70o,则它的其它两角的度数是。4.等腰直角三角形的每一个锐角都等于45°达标练习二(A水平)一、填空题:1、等腰三角形若两边长为3和7,则其周长为________。2、如果等腰三角形的一个底角为50°,那么其余两个角为______和______。3、如果等腰三角形的顶角为80°,那么它的一个底角为________。4、等腰三角形的底角可以是直角或钝角吗?为什么?二、判断题:1、等腰三角形的底角都是锐角()2、钝角三角形不可能是等腰三角形()√×1750°80°50°达标练习二(B水平)1、若等腰三角形的一个内角为40°,则它的另外两个内角为__________________2、若等腰三角形的一个内角为120°,则它的另外两个内角为______70°,70°或40°,100°30°,30°①顶角+2×底角=180°②顶角=180°-2×底角③底角=(180°-顶角)÷2结论:在等腰三角形中,已知一个角,就可以...