（课件）17平方差公式VIP免费

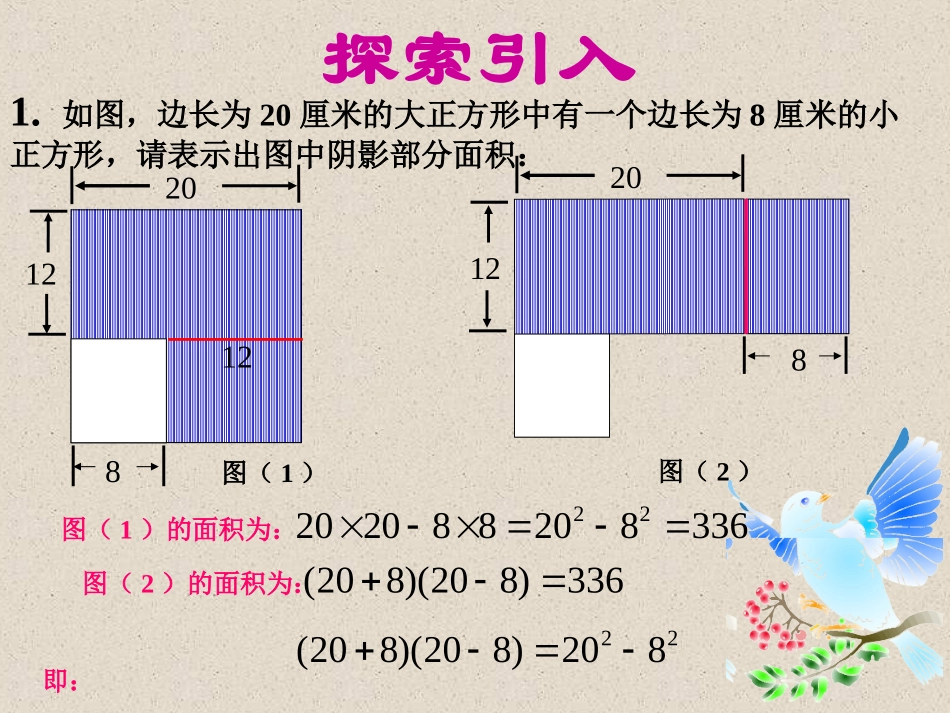
208图（1）探索引入1.如图，边长为20厘米的大正方形中有一个边长为8厘米的小正方形，请表示出图中阴影部分面积：图（1）的面积为：33682088202022图（2）的面积为：336)820)(820(即：22820)820)(820(121220图（2）8124222222xxxx2291)3(331aaaa从上式中你能发现一些有趣的现象吗？再举几个数试试.如果是一个数和一个字母，或两个都是字母呢？它们的情况又如何？2.计算下列各题：(1)(x+2)(x-2)(2)(1+3a)(1-3a)(3)(x+5y)(x-5y)(4)(y+3z)(y-3z)222225)5(55yxyxyxyx22229)3(33zyzyzyzy3、观察以上算式及其计算结果，你发现了什么规律？能不能大胆猜测得出一个一般性的结论？规律：1）左边是两个二项式相乘；2）在两个二项式中有一项完全相同，另一项互为相反数；3）右边为相同项的平方减互为相反数的项的平方.平方差公式现在要对大家提出的猜想进行证明，我们将证明过程演示给大家.证明：(a+b)(a-b)22bababa22ba我们经历了由发现——猜测——证明的过程，最后得出一个公式性的结论，我们将这个公式叫做平方差公式.22ba即：（a+b)(a-b)两数和与这两数差的积，等它们的平方差.（多项式乘法法则）（合并同类项）公式的应用例1、用平方差公式计算下列各题)65)(65(xx（1）（2）)2)(2(yxyxab(1)(5+6x)(5-6x)a(2)(x-2y)(x+2y)b2222)6(5xba23625x2222)2(yxba224yx分析：要利用平方差公式解题，必须找到相同的项和互为相反数的项，结果为相同项的平方减互为相反数的项的平方.ba例2、用平方差公式计算下列各题(-m+n)(-m-n)(1)(-m+n)(-m-n)解：22)())((nmnmnm(2)(-2x-5y)(5y-2x)解：22)5()2()25)(52(yxxyyx(3)(ab+8)(-ab+8)解：22)(8)8)(8(ababab前面两个例题可以直接套用平方差公式，可是不要“得意忘形”，现在让我们来看看下面一个例题.22nm22254yx2264ba例3、下列计算对不对？如果不对，怎样改正？4422222)2)(2(bababa2)366)6)(6(222xxxx错6)6)(6(2xxx1)分析：最后结果应是两项的平方差错44222222224)()2()2)(2(babababa3)2222425)2()5()25)(25(babababa分析：应是相同项的平方减互为相反数的项的平方错2222254)5()2()25)(25(ababbaba4)2291)3(1)31)(31(xxxx分析：不满足平方差公式的特点，没有相同项16933331)31)(31(2xxxxxxxx错分析：应将当作一个整体，用括号括起来再平方22a现在我们来看看平方差公式在混合运算中的运用：例4、计算23))((nnmnm分析：在混合运算中，观察是否有可以运用平方差公式的项先进行计算，将计算结果用括号括起来，避免符号出错.224nm2223)(nnm23))((nnmnm解：（平方差公式）（合并同类项）2223nnm（去括号）1.（1）（3m+2n)(3m-2n）（2）(b+2a)(2a-b)（3）（4）（-4a-1)(4a-1))221)(221(yxyx练习小结1、平方差公式是特殊的多项式乘法，要理解并掌握公式的结构特征.2、在混合运算中，用平方差公式直接计算所得的结果可以写在一个括号里，以免发生符号错误.2)右边是相同项的平方减互为相反数的项的平方.1)左边是两个二项式相乘，其中一项完全相同，另一项互为相反数.