指数及指数函数--完整版VIP免费

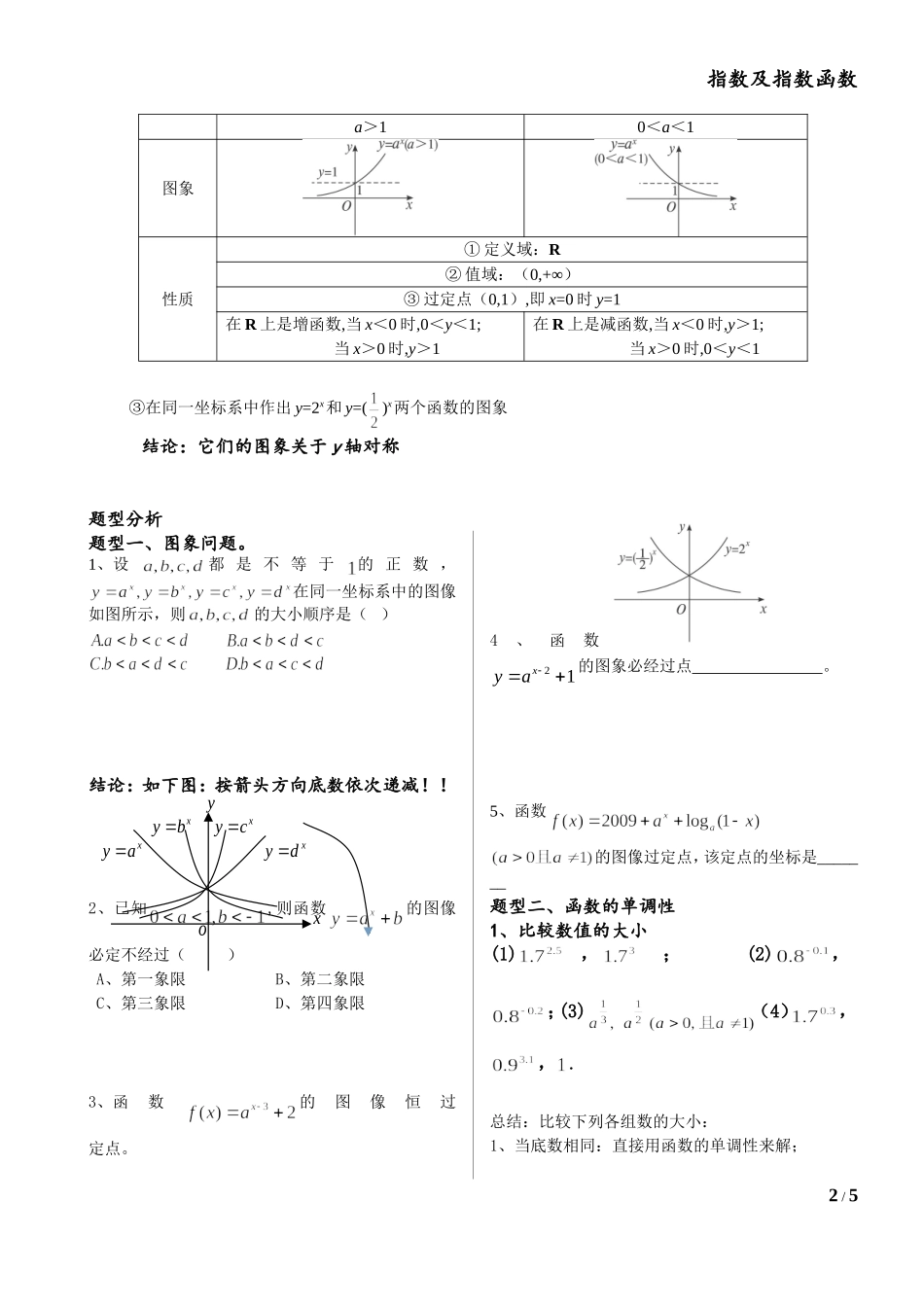
指数及指数函数指数及指数函数一、指数与指数运算（1）根式的概念：①定义：若，则称的次方根，1nnN且1）当为奇数时，次方根记作；2）当为偶数时，负数没有次方根，而正数有两个次方根且互为相反数，记作②性质：1）；2）当为奇数时，；3）当为偶数时(0)||(0)nnaaaaaa（2）幂的有关概念①规定：1）*()naaaanN；2）；3）1()ppapQa；4）、N*且②性质：1）、Q）；2）、Q）；3）Q）。（注）上述性质对r、R均适用。（3）巩固练习1.计算2.5.已知，求的值已知，求的值二、指数函数①定义：函数称指数函数.②指数函数y=ax在底数a＞1及0＜a＜1这两种情况下的图象和性质如下表所示：1/534．化简＋＝．．化简＝．112307210233abbaab指数及指数函数a＞10＜a＜1图象性质①定义域：R②值域：（0,+∞）③过定点（0,1）,即x=0时y=1在R上是增函数,当x＜0时,0＜y＜1;当x＞0时,y＞1在R上是减函数,当x＜0时,y＞1;当x＞0时,0＜y＜1③在同一坐标系中作出y=2x和y=()x两个函数的图象结论：它们的图象关于y轴对称题型分析题型一、图象问题。1、设都是不等于的正数，在同一坐标系中的图像如图所示，则的大小顺序是（）结论：如下图：按箭头方向底数依次递减！！2、已知,则函数的图像必定不经过（）A、第一象限B、第二象限C、第三象限D、第四象限3、函数的图像恒过定点。4、函数21xya的图象必经过点。5、函数的图像过定点，该定点的坐标是_______题型二、函数的单调性1、比较数值的大小(1)，；(2)，；(3)（4），，．总结：比较下列各组数的大小：1、当底数相同：直接用函数的单调性来解；2/5xayxbyxcyxdyxyo指数及指数函数2、当底数不同不能直接比较时：借助中间数（0或1），间接比较上述两个数的大小；练习：（一）比较下列各组数的大小（1）0.17()4和0.27()4；（2）163()4和；（3）2(0.8)和125()3(4)和（二）已知，函数，若实数满足，则的大小关系为____________2、求复合函数的单调性（1）求函数的单调递减区间；练习：求函数的单调递减区间；3、利用单调性解不等式（1）解不等式：（2）解关于的不等式（）（3）解关于的不等式4、利用单调性求参数的范围（1）函数在上是减函数，求取值范围；（2）函数在上的最大值比最小值大，则的值；（3）若直线与函数的图象有两个公共点，求的取值范围；（4）若函数，在上单调递减，求的取值范围；（5）已知，，若对任意，存在，使得，求实数的取值范围；题型三：利用指数函数转化为二次型函数1、已知，求的最值；2、已知当其值域为时，求的取值范围；3/5指数及指数函数题型四：利用指数函数限制范围求值域1、求函数11xxeye的值域；2、求函数2(0)21xxyx的值域题型五：函数奇偶性（1）函数()fx是奇函数,且当0x时,()1xfxe,求xR时,()fx（2）设0,()xxeaafxae是R上的偶函数,求值；练习：（1）定义在R上的函数()fx是奇函数,且当0x时,()1xfxe,则xR时,()fx__________．（2）已知函数1()21xfxa,若()fx为奇函数,则a________________．（3）设，，试确定的值，使为奇函数。题型六：综合应用1、已知函数,(1)判断函数的奇偶性；(2)求该函数的值域；(3)证明是上的增函数；练习：已知函数31()(1,0)31xxfxaa（1）求()fx的定义域和值域；（2）讨论()fx单调性；3、已知定义域为的函数是奇函数。（1）求的值（2）证明：函数在上是减函数（3）若对任意的，不等式恒成立，求的取值范围4/5指数及指数函数巩固练习1、如果函数的定义域为,那么的取值范围是A.B.C.D.2、函数的图象必经过点A.（0，1）B.（1，1）C.（2，1）D.（2，2）3、若函数在上的最大值与最小值之和为3，则函数在上的最大值是A.6B.1C.3D.4、设()2xfx，那么()fx是A奇函数且在上是增函数B偶函数且在上是增函数C奇函数且在上是减函数D偶函数且在上是减函数5、若函数15xym的图象不经过第二象限，则m的取值范围是_________6、若，则=.7、已知则8、求2()25,[1,2],(01)xxfxaaxaa且的值域和单调区间.5/5